题目内容
函数f(x)=x2+2x+5在[t,t+1]上的最小值为
(t）,求(t)的表达式。
f(x)=x2+2x+5=(x+1)2+4.当t>-1时，f(x)的最小值为t2+2t+5;当-2
时，f(x)的最小值为4；当t<-2时，f(x)的最小值为t2+4t+8。
∴
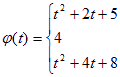
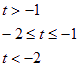
解析:
分类讨论对称轴与区间的关系来求最值
练习册系列答案
相关题目
已知函数f(x)=
若f（2-a2）＞f（a），则实数a的取值范围是（ ）
|
| A、（-∞，-1）∪（2，+∞） |
| B、（-1，2） |
| C、（-2，1） |
| D、（-∞，-2）∪（1，+∞） |