题目内容
在斜三角形ABC中, ,且
,且 ,则∠A的值为
,则∠A的值为
- A.

- B.

- C.

- D.

A
分析:由条件可得 sinBcosC+cosBsinC=- cosBcosC,两边同除cosBcosC可得 tanB+tanC的值,再利用两角和的正切公式求得tan(B+C)的值,可得B+C的值,从而得到A的值.
cosBcosC,两边同除cosBcosC可得 tanB+tanC的值,再利用两角和的正切公式求得tan(B+C)的值,可得B+C的值,从而得到A的值.
解答:∵在斜三角形ABC中,sinA=sin(B+C)=sinBcosC+cosBsinC=- cosBcosC,
cosBcosC,
两边同除cosBcosC可得 tanB+tanC=- .
.
又tanBtanC=1- ,
,
所以tan(B+C)=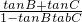 =-1,
=-1,
∴B+C= ,A=
,A= .
.
故选A.
点评:本题主要考查同角三角函数的基本关系,两角和的正弦公式、正切公式、诱导公式的应用,已知三角函数值求角的大小,属于中档题.
分析:由条件可得 sinBcosC+cosBsinC=-
 cosBcosC,两边同除cosBcosC可得 tanB+tanC的值,再利用两角和的正切公式求得tan(B+C)的值,可得B+C的值,从而得到A的值.
cosBcosC,两边同除cosBcosC可得 tanB+tanC的值,再利用两角和的正切公式求得tan(B+C)的值,可得B+C的值,从而得到A的值.解答:∵在斜三角形ABC中,sinA=sin(B+C)=sinBcosC+cosBsinC=-
 cosBcosC,
cosBcosC,两边同除cosBcosC可得 tanB+tanC=-
 .
.又tanBtanC=1-
 ,
,所以tan(B+C)=
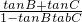 =-1,
=-1,∴B+C=
 ,A=
,A= .
.故选A.
点评:本题主要考查同角三角函数的基本关系,两角和的正弦公式、正切公式、诱导公式的应用,已知三角函数值求角的大小,属于中档题.

练习册系列答案
相关题目
 cos B·cos C,且tan
B·tan C=1-
cos B·cos C,且tan
B·tan C=1- B.
B.
 D.
D.