题目内容
(本小题满分16分)已知函数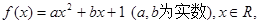
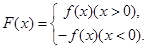
(1)若不等式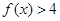 的解集为
的解集为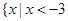 或
或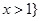 ,求
,求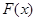 的表达式;
的表达式;
(2)在(1)的条件下, 当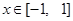 时,
时, 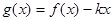 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设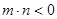 ,
, 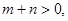
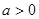 且
且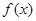 为偶函数, 判断
为偶函数, 判断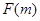 +
+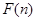 能否大于零?
能否大于零?
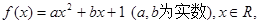
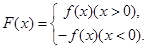
(1)若不等式
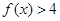 的解集为
的解集为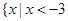 或
或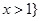 ,求
,求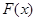 的表达式;
的表达式;(2)在(1)的条件下, 当
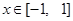 时,
时, 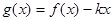 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;(3)设
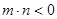 ,
, 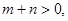
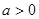 且
且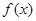 为偶函数, 判断
为偶函数, 判断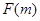 +
+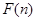 能否大于零?
能否大于零?(1)由已知不等式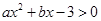 的解集为
的解集为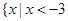 或
或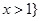 ,故
,故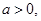 且方程
且方程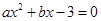 的两根为
的两根为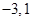 ,由韦达定理,得
,由韦达定理,得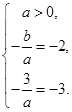 解得
解得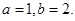 因此,
因此,
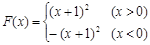
(2) 则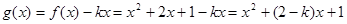
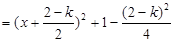 ,
,
当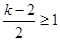 或
或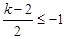 时, 即
时, 即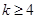 或
或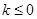 时,
时, 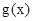 是单调函数.
是单调函数.
(3) ∵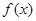 是偶函数∴
是偶函数∴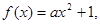
 ,
,
∵ 设
设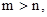 则
则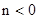 .又
.又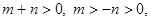 ∴
∴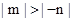
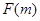 +
+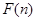
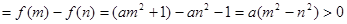 ,
,
∴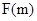 +
+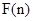 能大于零
能大于零
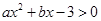 的解集为
的解集为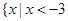 或
或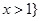 ,故
,故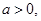 且方程
且方程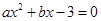 的两根为
的两根为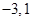 ,由韦达定理,得
,由韦达定理,得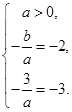 解得
解得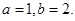 因此,
因此,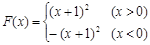
(2) 则
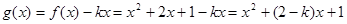
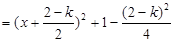 ,
, 当
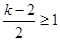 或
或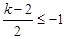 时, 即
时, 即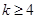 或
或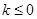 时,
时, 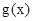 是单调函数.
是单调函数.(3) ∵
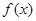 是偶函数∴
是偶函数∴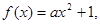
 ,
, ∵
 设
设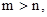 则
则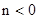 .又
.又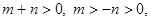 ∴
∴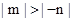
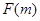 +
+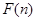
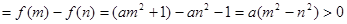 ,
,∴
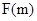 +
+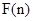 能大于零
能大于零略

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
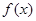 是定义在
是定义在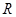 上的奇函数,当
上的奇函数,当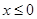 时,
时,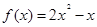 ,则
,则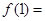 ( )
( )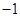
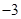
 是奇函数,则
是奇函数,则
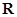 上的函数
上的函数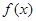 满足
满足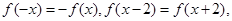 且
且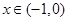 时
时 则
则 ( )
( ) 
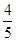
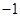
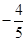
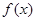 是定义在R上的奇函数,若当
是定义在R上的奇函数,若当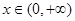 时,
时,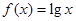 ,则满足
,则满足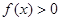 的
的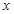 的取值范围是( )
的取值范围是( )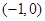
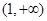
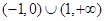
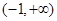
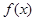 为偶函数,且当
为偶函数,且当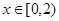 时
时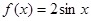 ,当
,当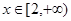 时
时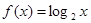 ,则
,则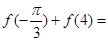 ( )
( )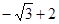

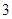

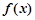 是偶函数,当
是偶函数,当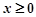 时,
时, 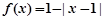 ,满足
,满足 的实数
的实数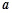 的个数为_____________个
的个数为_____________个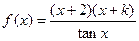 为奇函数,则
为奇函数,则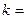
 上的函数
上的函数 是偶函数,则实数
是偶函数,则实数