题目内容
已知函数 .
.
(1)求f(x)的最大值与最小值;
(2)若α-β≠kπ,k∈Z,且f(α)=f(β),求tan(α+β)的值.
解:(1)由f(0)=2a=2,得a=1,由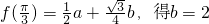 ,
,
∴f(x)=2cos2x+2sinxcosx=sin2x+cos2x+1= ,
,
∴f(x)的最大值是 ,最小值是
,最小值是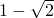 .
.
(2)∵f(α)=f(β),∴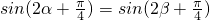 .
.
∴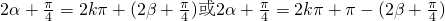 ,
,
∴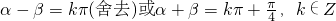 ,∴
,∴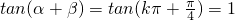 .
.
分析:(1)由f(0)=2 求得a值,由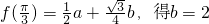 ,化简f(x)=
,化简f(x)= ,可得最值.
,可得最值.
(2)f(α)=f(β),可得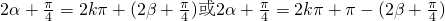 ,得到α+β的值,从而求得tan(α+β)的值.
,得到α+β的值,从而求得tan(α+β)的值.
点评:本题考查两角和的正弦、正切公式的应用,以及正弦函数的值域,得到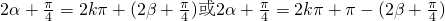 是解题的难点.
是解题的难点.
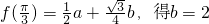 ,
,∴f(x)=2cos2x+2sinxcosx=sin2x+cos2x+1=
 ,
,∴f(x)的最大值是
 ,最小值是
,最小值是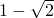 .
.(2)∵f(α)=f(β),∴
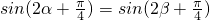 .
.∴
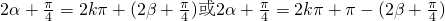 ,
,∴
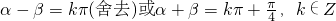 ,∴
,∴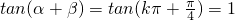 .
.分析:(1)由f(0)=2 求得a值,由
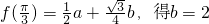 ,化简f(x)=
,化简f(x)= ,可得最值.
,可得最值.(2)f(α)=f(β),可得
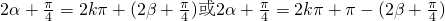 ,得到α+β的值,从而求得tan(α+β)的值.
,得到α+β的值,从而求得tan(α+β)的值.点评:本题考查两角和的正弦、正切公式的应用,以及正弦函数的值域,得到
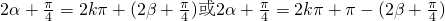 是解题的难点.
是解题的难点. 
练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.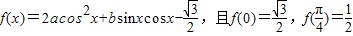 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.