Question

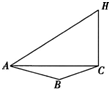为了应对日益严重的气候问题，某气象仪器科研单位研究出一种新的“弹射型”气象仪器，这种仪器可以弹射到空中进行气象观测．如图所示，A，B，C三地位于同一水平面上，这种仪器在C地进行弹射实验，观测点A，B两地相距100米，∠BAC=60°在A地听到弹射声音的时间比B地晚

2

17

秒．在A地测得该仪器至最高点H处的仰角为30°．
（1）求A，C两地的距离；
（2）求这种仪器的垂直弹射高度HC（已知声音的传播速度为340米∕秒）

Answer 1

分析：（1）利用在A地听到弹射声音的时间比B地晚

2

17

秒，求出BC，利用余弦定理，即可求得结论；
（2）在△ACH中，AC=420，∠CAH=30°，利用正弦函数，可得结论．

解答：解：（1）由题意，设AC=x，则
∵在A地听到弹射声音的时间比B地晚

2

17

秒
∴BC=x-

2

17

×340=x-40，
在△ABC内，由余弦定理：BC²=BA²+CA²-2BA•CA•cos∠BAC，
即（x-40）²=x²+10000-100x，解得x=420．
（2）在△ACH中，AC=420，∠CAH=30°，
∴CH=AC•sin∠CAH=210米．
答：该仪器的垂直弹射高度CH为210米．

点评：本题考查余弦定理的运用，考查学生利用数学知识解决实际问题的能力，考查学生分析解决问题的能力，属于中档题．