题目内容
点M的直角坐标为 ,则点M的极坐标为( )
,则点M的极坐标为( )A.

B.

C.

D.

【答案】分析:根据点M的直角坐标是(-1,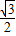 ),利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,求得ρ和θ的值,即可求得它的极坐标(ρ,θ).
),利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,求得ρ和θ的值,即可求得它的极坐标(ρ,θ).
解答:解:由于点M的直角坐标为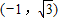 ,设M的极坐标为(ρ,θ),
,设M的极坐标为(ρ,θ),
由于ρ2=x2+y2,可得:ρ2=4,∴ρ=2.
由于极角θ满足cosθ=- ,sinθ=
,sinθ=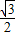 ,故θ为第二象限角,故θ=
,故θ为第二象限角,故θ=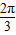 ,
,
故点M的极坐标为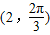 ,
,
故选C.
点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得,属于基础题.
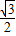 ),利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,求得ρ和θ的值,即可求得它的极坐标(ρ,θ).
),利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,求得ρ和θ的值,即可求得它的极坐标(ρ,θ).解答:解:由于点M的直角坐标为
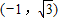 ,设M的极坐标为(ρ,θ),
,设M的极坐标为(ρ,θ),由于ρ2=x2+y2,可得:ρ2=4,∴ρ=2.
由于极角θ满足cosθ=-
 ,sinθ=
,sinθ=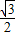 ,故θ为第二象限角,故θ=
,故θ为第二象限角,故θ=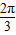 ,
,故点M的极坐标为
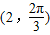 ,
,故选C.
点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得,属于基础题.

练习册系列答案
相关题目
点M的直角坐标为(-1,-1,
),则它的球坐标为( )
| 2 |
A、(2,
| ||||
B、(2,
| ||||
C、(2,
| ||||
D、(2,
|
 ,则它的柱坐标为( )
,则它的柱坐标为( )



 ,则点M的极坐标为 .
,则点M的极坐标为 . ,则它的球坐标为( )
,则它的球坐标为( )


