题目内容
递减的等差数列{an}的前n项和为Sn.若a3•a5=63,a2+a6=16,
(1)求{an}的通项公式
(2)当n为多少时,Sn取最大值,并求其最大值.
(3)求|a1|+|a2|+|a3|+…+|an|.
解:(1)a2+a6=a3+a5=16,又a3•a5=63,
所以a3与a5是方程x2-16x+63=0的两根,
解得 ,
,
又该等差数列递减,所以 ,
,
则公差d= ,a1=11,
,a1=11,
所以an=11+(n-1)(-1)=12-n;
(2)由 ,即
,即 ,解得11≤n≤12,
,解得11≤n≤12,
又n∈N*,所以当n=11或12时Sn取最大值,最大值为S11= =66;
=66;
(3)由(2)知,当n≤12时an≤0,当n>12时an>0,
①当n≤12时,
|a1|+|a2|+|a3|+…+|an|=-(a1+a2+a3+…+an)
=-Sn=-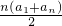 =-
=- =
= -
- ;
;
②当n>12时,
|a1|+|a2|+|a3|+…+|an|=-(a1+a2+a3+…+a12)+(a13+a14+…+an)
=Sn-2S12= -2×66=-
-2×66=- ;
;
所以|a1|+|a2|+|a3|+…+|an|= .
.
分析:(1)a2+a6=a3+a5=16,由此可把a3与a5看作方程x2-16x+63=0的两根,解出a3与a5,根据通项公式可得公差及首项;
(2)由递减等差数列性质可知,要使Sn取最大值,则有an≥0,an+1≤0,解出n,即可求得正整数n值;
(3)分①当n≤12时,②当n>12时两种情况进行讨论,借助等差数列前n项和公式即可求得答案;
点评:本题考查等差数列通项公式、前n项和公式及数列求和,考查分类讨论思想,熟练掌握等差数列的通项公式及前n项和公式是解决该类问题的基础.
所以a3与a5是方程x2-16x+63=0的两根,
解得
 ,
,又该等差数列递减,所以
 ,
,则公差d=
 ,a1=11,
,a1=11,所以an=11+(n-1)(-1)=12-n;
(2)由
 ,即
,即 ,解得11≤n≤12,
,解得11≤n≤12,又n∈N*,所以当n=11或12时Sn取最大值,最大值为S11=
 =66;
=66;(3)由(2)知,当n≤12时an≤0,当n>12时an>0,
①当n≤12时,
|a1|+|a2|+|a3|+…+|an|=-(a1+a2+a3+…+an)
=-Sn=-
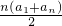 =-
=- =
= -
- ;
;②当n>12时,
|a1|+|a2|+|a3|+…+|an|=-(a1+a2+a3+…+a12)+(a13+a14+…+an)
=Sn-2S12=
 -2×66=-
-2×66=- ;
;所以|a1|+|a2|+|a3|+…+|an|=
 .
.分析:(1)a2+a6=a3+a5=16,由此可把a3与a5看作方程x2-16x+63=0的两根,解出a3与a5,根据通项公式可得公差及首项;
(2)由递减等差数列性质可知,要使Sn取最大值,则有an≥0,an+1≤0,解出n,即可求得正整数n值;
(3)分①当n≤12时,②当n>12时两种情况进行讨论,借助等差数列前n项和公式即可求得答案;
点评:本题考查等差数列通项公式、前n项和公式及数列求和,考查分类讨论思想,熟练掌握等差数列的通项公式及前n项和公式是解决该类问题的基础.

练习册系列答案
相关题目
在递减的等差数列{an}中,a2+a4+a6=12,a3•a5=7,前n项和为Sn
(1)求an;
(2)求Sn及其最值,并指明n的取值;
(3)令Tn=|a1|+|a2|+|a3|+…+|an|,求Tn.
(1)求an;
(2)求Sn及其最值,并指明n的取值;
(3)令Tn=|a1|+|a2|+|a3|+…+|an|,求Tn.
已知递减的等差数列{an}满足a12=a92,则数列{an}的前n项和Sn取最大值时,n=( )
| A、3 | B、4 | C、4或5 | D、5或6 |