题目内容
某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门。该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同。
(1求恰有2门选修课这3个学生都没有选择的概率;
(2设随机变量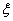 为甲、乙、丙这三个学生选修数学史这门课的人数,
为甲、乙、丙这三个学生选修数学史这门课的人数,
求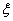 的分布列及期望,方差.
的分布列及期望,方差.
(1)恰有2门选修课这3个学生都没有选择的概率:
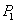 =
=
(Ⅲ)设数学史这门课这3个学生选择的人数为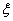 ,则
,则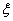 =0,1,2,3
=0,1,2,3
P (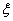 = 0 ) =
= 0 ) =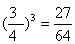 P (
P (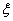 = 1) =
= 1) =
P (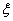 = 2 ) =
= 2 ) = P (
P (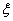 = 3 ) =
= 3 ) =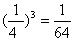
∴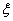 的分布列为:
的分布列为:
|
| 0 | 1 | 2 | 3 |
| P |
|
|
|
|
∴期望E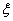 =np=
=np= ,
,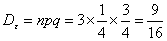

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
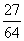
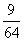


 B.
B.
 D.
D.
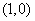 的直线与曲线
的直线与曲线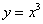 和
和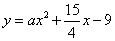 都相切,则
都相切,则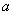 等于 ( )
等于 ( )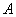 .
.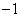 或
或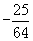
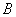 .
.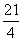
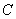 .
.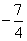 或
或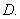
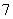
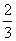 上移动,在点P处的切线的倾斜角为α,则α的取
上移动,在点P处的切线的倾斜角为α,则α的取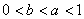 ,则在
,则在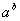 ,
,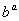 ,
,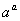 ,
,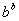 中最大值是( )
中最大值是( )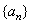 的前n项和为
的前n项和为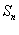 ,若
,若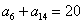 ,则
,则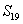 =______________.
=______________.  (m∈R,i为虚数单位)在复平面上对应的点不可能位于 ( )
(m∈R,i为虚数单位)在复平面上对应的点不可能位于 ( ) ,
, 的定义域都为R,且
的定义域都为R,且 .
. .|
.| .
. .|
.|