题目内容
 有一条长度为1的线段EF,其端点E、F在边长为3的正方形ABCD的四边滑动,当F绕着正方形的四边滑动一周时,EF的中点M所形成的轨迹长度最接近于
有一条长度为1的线段EF,其端点E、F在边长为3的正方形ABCD的四边滑动,当F绕着正方形的四边滑动一周时,EF的中点M所形成的轨迹长度最接近于
- A.8
- B.11
- C.12
- D.10
B
分析:首先当两点在正方形两边时,由两点间距离公式表示出|EF|,再利用中点坐标公式建立线段EF的中点M与其两端点的坐标关系,然后求出E、F在同一边AB时,点M的轨迹长,最后求出所求即可.
解答:当两点在正方形两边时,设F(m,0)、E(0,n),则|EF|2=m2+n2=1,
再设线段EF中点M的坐标为(x,y),则x= ,y=
,y= ,即m=2x,n=2y,
,即m=2x,n=2y,
所以4x2+4y2=1,即EF中点M的轨迹方程为x2+y2= .
.
在E、F同一边AB时,点M的轨迹长为2
∴当F绕着正方形的四边滑动一周时,EF的中点M所形成的轨迹长度为4( ×π+2)=π+8≈11
×π+2)=π+8≈11
故选B
点评:本题考查两点间距离公式、中点坐标公式及方程思想,属于中档题.
分析:首先当两点在正方形两边时,由两点间距离公式表示出|EF|,再利用中点坐标公式建立线段EF的中点M与其两端点的坐标关系,然后求出E、F在同一边AB时,点M的轨迹长,最后求出所求即可.
解答:当两点在正方形两边时,设F(m,0)、E(0,n),则|EF|2=m2+n2=1,
再设线段EF中点M的坐标为(x,y),则x=
 ,y=
,y= ,即m=2x,n=2y,
,即m=2x,n=2y,所以4x2+4y2=1,即EF中点M的轨迹方程为x2+y2=
 .
.在E、F同一边AB时,点M的轨迹长为2
∴当F绕着正方形的四边滑动一周时,EF的中点M所形成的轨迹长度为4(
 ×π+2)=π+8≈11
×π+2)=π+8≈11故选B
点评:本题考查两点间距离公式、中点坐标公式及方程思想,属于中档题.

练习册系列答案
相关题目
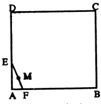 有一条长度为1的线段EF,其端点E、F在边长为3的正方形ABCD的四边滑动,当F绕着正方形的四边滑动一周时,EF的中点M所形成的轨迹长度最接近于( )
有一条长度为1的线段EF,其端点E、F在边长为3的正方形ABCD的四边滑动,当F绕着正方形的四边滑动一周时,EF的中点M所形成的轨迹长度最接近于( )


