题目内容
(本小题满分12分) 已知抛物线
已知抛物线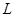 :
: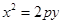 和点
和点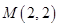 ,若抛物线
,若抛物线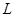 上存在不同两点
上存在不同两点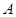 、
、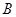 满足
满足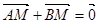 .
.
(I)求实数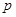 的取值范围;
的取值范围;
(II)当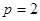 时,抛物线
时,抛物线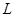 上是否存在异于
上是否存在异于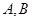 的点
的点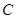 ,使得经过
,使得经过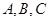 三点的圆和抛物线
三点的圆和抛物线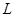 在点
在点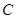 处有相同的切线,若存在,求出点
处有相同的切线,若存在,求出点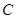 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
 已知抛物线
已知抛物线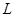 :
: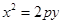 和点
和点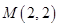 ,若抛物线
,若抛物线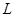 上存在不同两点
上存在不同两点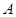 、
、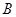 满足
满足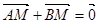 .
.(I)求实数
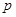 的取值范围;
的取值范围;(II)当
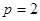 时,抛物线
时,抛物线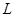 上是否存在异于
上是否存在异于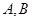 的点
的点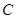 ,使得经过
,使得经过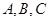 三点的圆和抛物线
三点的圆和抛物线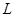 在点
在点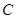 处有相同的切线,若存在,求出点
处有相同的切线,若存在,求出点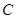 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.(1) 即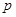 的取值范围为
的取值范围为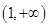 .
.
(2) 满足题设的点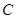 存在,其坐标为
存在,其坐标为 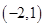 .
.
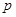 的取值范围为
的取值范围为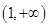 .
.(2) 满足题设的点
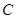 存在,其坐标为
存在,其坐标为 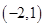 .
. 试题分析:解法1:(I)不妨设A
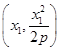 ,B
,B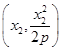 ,且
,且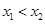 ,∵
,∵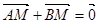 ,
,∴
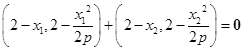 .∴
.∴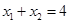 ,
,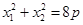 .
. 根据基本不等式
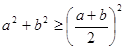 (当且仅当
(当且仅当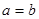 时取等号)得
时取等号)得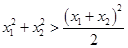 (
(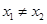 ),即
),即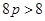 ,
,∴
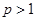 ,即
,即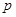 的取值范围为
的取值范围为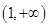 .
. (II)当
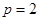 时,由(I求得
时,由(I求得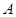 、
、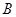 的坐标分别为
的坐标分别为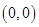 、
、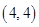 .
. 假设抛物线
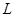 上存在点
上存在点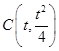 (
(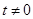 ,且
,且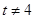 ),使得经过
),使得经过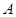 、
、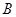 、
、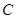 三点的圆和抛物线
三点的圆和抛物线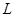 在点
在点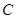 处有相同的切线.
处有相同的切线.设经过
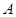 、
、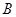 、
、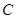 三点的圆的方程为
三点的圆的方程为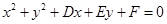 ,
, 则
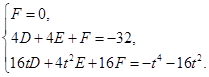
整理得
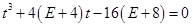 . ①
. ①∵函数
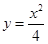 的导数为
的导数为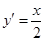 ,
,∴抛物线
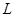 在点
在点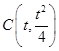 处的切线的斜率为
处的切线的斜率为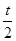 ,
,∴经过
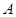 、
、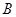 、
、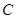 三点的圆
三点的圆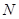 在点
在点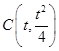 处的切线斜率为
处的切线斜率为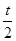 .
.∵
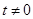 ,∴直线
,∴直线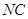 的斜率存在.∵圆心
的斜率存在.∵圆心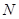 的坐标为
的坐标为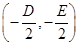 ,
, ∴
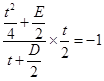 ,即
,即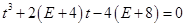 . ②
. ②∵
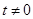 ,由①、②消去
,由①、②消去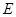 ,得
,得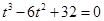 . 即
. 即 .
.∵
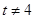 ,∴
,∴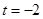 .故满足题设的点
.故满足题设的点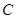 存在,其坐标为
存在,其坐标为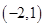 .
. 解法2:(I)设
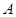 ,
,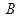 两点的坐标为
两点的坐标为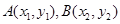 ,且
,且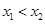 。
。∵
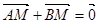 ,可得
,可得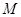 为
为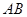 的中点,即
的中点,即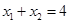 .
. 显然直线
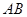 与
与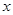 轴不垂直,设直线
轴不垂直,设直线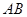 的方程为
的方程为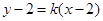 ,即
,即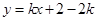 ,将
,将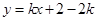 代入
代入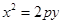 中,
中,得
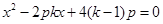 .∴
.∴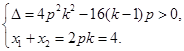
∴
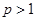 . 故
. 故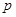 的取值范围为
的取值范围为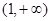 .
.(II)当
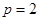 时,由(1)求得
时,由(1)求得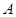 ,
,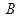 的坐标分别为
的坐标分别为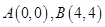 .
. 假设抛物线
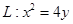 上存在点
上存在点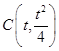 (
(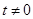 且
且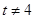 ),使得经过
),使得经过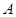 、
、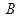 、
、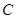 三点的圆和抛物线
三点的圆和抛物线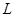 在点
在点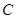 处有相同的切线.
处有相同的切线. 设圆的圆心坐标为
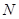
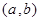 ,
, ∵
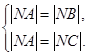 ∴
∴
即
 解得
解得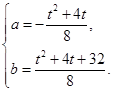
∵抛物线
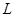 在点
在点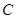 处切线的斜率为
处切线的斜率为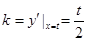 ,而
,而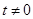 ,且该切线与
,且该切线与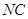 垂直,
垂直,∴
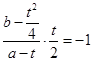 ,即
,即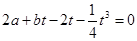 .将
.将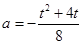 ,
, 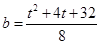
代入上式,得
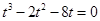 ,即
,即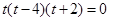 .
.∵
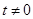 且
且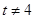 ,∴
,∴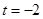 .
.故满足题设的点
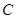 存在,其坐标为
存在,其坐标为 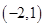 .
.点评:解决该试题的关键是利用抛物线的方程以及性质来分析得到结论,同时对于探索性问题,一般先假设,然后分析求解,属于中档题。

练习册系列答案
相关题目
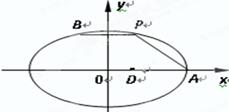
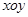 中,点
中,点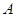 为椭圆
为椭圆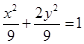 的右顶点, 点
的右顶点, 点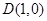 ,点
,点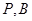 在椭圆上,
在椭圆上, 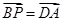 .
.
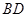 的方程;
的方程;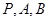 三点的圆
三点的圆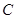 截得的弦长;
截得的弦长;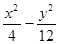 =1的焦点到渐近线的距离为( )。
=1的焦点到渐近线的距离为( )。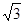
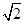 ,离心率e=
,离心率e=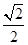 ,过右焦点F的直线l交椭圆于P、Q两点.
,过右焦点F的直线l交椭圆于P、Q两点.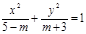 是椭圆”
是椭圆”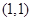 和直线
和直线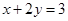 距离相等的点的轨迹是直线
距离相等的点的轨迹是直线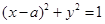 与双曲线
与双曲线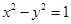 的渐近线相切,则
的渐近线相切,则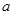 的值是 _______.
的值是 _______. 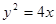 的焦点为F,过抛物线在第一象限部分上一点P的切线为
的焦点为F,过抛物线在第一象限部分上一点P的切线为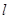 ,过P点作平行于
,过P点作平行于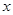 轴的直线
轴的直线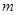 ,过焦点F作平行于
,过焦点F作平行于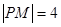 ,则点P的坐标为 。
,则点P的坐标为 。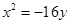 的焦点相同,则双曲线C的标准方程是( )
的焦点相同,则双曲线C的标准方程是( )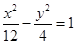
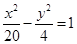
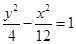
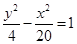
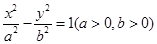 的一条渐近线经过点
的一条渐近线经过点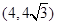 ,则该双曲线的离心率为___________.
,则该双曲线的离心率为___________.