题目内容
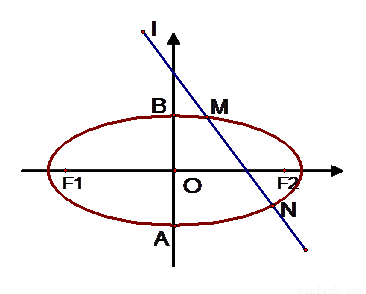
如图所示,椭圆C: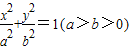 的离心率
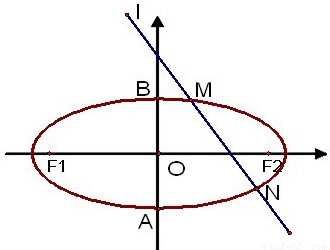
的离心率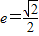 ,左焦点为F1(-1,0),右焦点为F2(1,0),短轴两个端点为A、B.与x轴不垂直的直线l与椭圆C交于不同的两点M、N,记直线AM、AN的斜率分别为k1、k2,且
,左焦点为F1(-1,0),右焦点为F2(1,0),短轴两个端点为A、B.与x轴不垂直的直线l与椭圆C交于不同的两点M、N,记直线AM、AN的斜率分别为k1、k2,且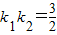 .
.(1)求椭圆C的方程;
(2)求证直线l与y轴相交于定点,并求出定点坐标.
(3)当弦MN的中点P落在△MF1F2内(包括边界)时,求直线l的斜率的取值.
【答案】分析:(1)由焦点坐标可得c值,由离心率可得a值,据a,b,c关系可求得b;
(2)设直线l的方程为y=kx+b,M、N坐标分别为 M(x1,y1),N(x2,y2),联立直线方程与椭圆方程消掉y得x的二次方程,由韦达定理及斜率公式可用k,b表示出等式 ,由此可求得b值,进而可求得直线所过定点;
,由此可求得b值,进而可求得直线所过定点;
(3)由(2)中的一元二次方程可求得判别式大于0求得k的范围,设弦AB的中点P坐标则可分别表示出x和y,易判断p点在x轴上方,从而得一关于x,y的不等式组,将坐标代入,解出即可;
解答:解:(1)由题意可知:椭圆C的离心率 ,c=1,∴b2=1,a2=2,
,c=1,∴b2=1,a2=2,
故椭圆C的方程为 .
.
(2)设直线l的方程为y=kx+b,M、N坐标分别为 M(x1,y1),N(x2,y2),
由 得(1+2k2)x2+4kbx+2b2-2=0,
得(1+2k2)x2+4kbx+2b2-2=0,
∴ ,
,
∵ .
.
∴ ,
,
将韦达定理代入,并整理得 ,解得b=2.
,解得b=2.
∴直线l与y轴相交于定点(0,2);
(3)由(2)中(1+2k2)x2+4kbx+2b2-2=(1+2k2)x2+8kx+6=0,其判别式△>0,得 .①
.①
设弦AB的中点P坐标为(x,y),则 ,
,
∵弦MN的中点P落在△MF1F2内(包括边界),∴
将坐标代入,整理得
解得 ②,
②,
由①②得所求范围为 ;
;
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生转化与化归思想的运用和基础知识的熟练掌握.
(2)设直线l的方程为y=kx+b,M、N坐标分别为 M(x1,y1),N(x2,y2),联立直线方程与椭圆方程消掉y得x的二次方程,由韦达定理及斜率公式可用k,b表示出等式
 ,由此可求得b值,进而可求得直线所过定点;
,由此可求得b值,进而可求得直线所过定点;(3)由(2)中的一元二次方程可求得判别式大于0求得k的范围,设弦AB的中点P坐标则可分别表示出x和y,易判断p点在x轴上方,从而得一关于x,y的不等式组,将坐标代入,解出即可;
解答:解:(1)由题意可知:椭圆C的离心率
 ,c=1,∴b2=1,a2=2,
,c=1,∴b2=1,a2=2,故椭圆C的方程为
 .
.(2)设直线l的方程为y=kx+b,M、N坐标分别为 M(x1,y1),N(x2,y2),
由
 得(1+2k2)x2+4kbx+2b2-2=0,
得(1+2k2)x2+4kbx+2b2-2=0,∴
 ,
,∵
 .
.∴
 ,
,将韦达定理代入,并整理得
 ,解得b=2.
,解得b=2.∴直线l与y轴相交于定点(0,2);
(3)由(2)中(1+2k2)x2+4kbx+2b2-2=(1+2k2)x2+8kx+6=0,其判别式△>0,得
 .①
.①设弦AB的中点P坐标为(x,y),则
 ,
,∵弦MN的中点P落在△MF1F2内(包括边界),∴

将坐标代入,整理得

解得
 ②,
②,由①②得所求范围为
 ;
;点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生转化与化归思想的运用和基础知识的熟练掌握.

练习册系列答案
相关题目
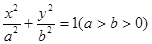 的离心率
的离心率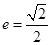 ,左焦点为
,左焦点为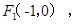 右焦点为
右焦点为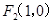 ,短轴两个端点为
,短轴两个端点为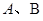 .与
.与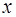 轴不垂直的直线
轴不垂直的直线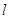 与椭圆C交于不同的两点
与椭圆C交于不同的两点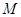 、
、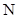 ,记直线
,记直线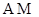 、
、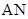 的斜率分别为
的斜率分别为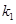 、
、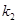 ,且
,且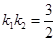 .
.
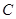 的方程;
的方程;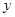 轴相交于定点,并求出定点坐标.
轴相交于定点,并求出定点坐标. 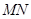 的中点
的中点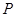 落在
落在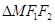 内(包括边界)时,求直线
内(包括边界)时,求直线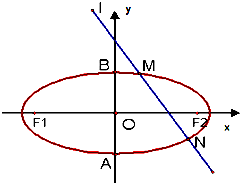 如图所示,椭圆C:
如图所示,椭圆C: 的离心率
的离心率 ,左焦点为F1(-1,0)右焦点为F2(1,0),短轴两个端点为A、B,与x轴不垂直的直线l与椭圆C交于不同的两点M、N,记直线AM、AN的斜率分别为k1,k2,且
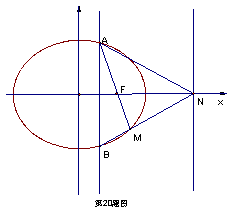
,左焦点为F1(-1,0)右焦点为F2(1,0),短轴两个端点为A、B,与x轴不垂直的直线l与椭圆C交于不同的两点M、N,记直线AM、AN的斜率分别为k1,k2,且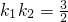 .
.
 如图所示,椭圆C:
如图所示,椭圆C: 。
。