题目内容
4、函数f(x)、g(x)在R上可导,且f′(x)>g′(x),若a>b,则( )
分析:先将f′(x)>g′(x)转化为)[f(x)-g(x)]'>0得到函数F(x)=f(x)-g(x)是单调递增函数,再由当a>b时,得到
F(a)>F(b)成立可得到答案.
F(a)>F(b)成立可得到答案.
解答:解:∵f′(x)>g′(x),∴[f(x)-g(x)]'>0
∴函数F(x)=f(x)-g(x)是单调递增函数
当a>b时,得到F(a)>F(b)成立,即f(a)-g(a)>f(b)-g(b)
∴f(a)-f(b)>g(a)-g(b)
故选D.
∴函数F(x)=f(x)-g(x)是单调递增函数
当a>b时,得到F(a)>F(b)成立,即f(a)-g(a)>f(b)-g(b)
∴f(a)-f(b)>g(a)-g(b)
故选D.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系.属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
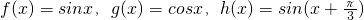 ;
;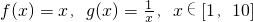 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围. ;
; 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.