题目内容
极坐标系的极点为直角坐标系xOy的原点,极轴为z轴的正半轴,两种坐标系的长度单位相同,己知圆C1的极坐标方程为p=4(cosθ+sinθ),P是C1上一动点,点Q在射线OP上且满足
OQ= OP,点Q的轨迹为C2.
OP,点Q的轨迹为C2.
(I)求曲线C2的极坐标方程,并化为直角坐标方程;
( II)已知直线l的参数方程为 (t为参数,0≤φ<π),l与曲线C2有且只有一个公共点,求φ的值.
(t为参数,0≤φ<π),l与曲线C2有且只有一个公共点,求φ的值.
OQ=
 OP,点Q的轨迹为C2.
OP,点Q的轨迹为C2.(I)求曲线C2的极坐标方程,并化为直角坐标方程;
( II)已知直线l的参数方程为
 (t为参数,0≤φ<π),l与曲线C2有且只有一个公共点,求φ的值.
(t为参数,0≤φ<π),l与曲线C2有且只有一个公共点,求φ的值.解:(Ⅰ)设点P、Q的极坐标分别为(ρ0,θ)、(ρ,θ),
则 ρ=  ρ0=
ρ0=  ×4(cosθ+sinθ)=2(cosθ+sinθ),
×4(cosθ+sinθ)=2(cosθ+sinθ),
点Q轨迹C2的极坐标方程为ρ=2(cosθ+sinθ),
两边同乘以ρ,得ρ2=2(ρcosθ+ρsinθ),
C2的直角坐标方程为x2+y2=2x+2y,
即(x﹣1)2+(y﹣1)2=2.
(Ⅱ)将l的代入曲线C2的直角坐标方程,
得(tcosφ+1)2+(tsinφ﹣1)2=2,
即t2+2(cosφ﹣sinφ)t=0,
t1=0,t2=sinφ﹣cosφ,
由直线l与曲线C2有且只有一个公共点,
得sinφ﹣cosφ=0,
因为0≤φ<π,
所以φ= .
.

练习册系列答案
相关题目
 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线 的极坐标方程为
的极坐标方程为 .
. (
( 为参数)与曲线C交于
为参数)与曲线C交于 ,
, 两点,与
两点,与 轴交于
轴交于 ,求
,求 的值.
的值.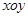 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线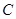 的极坐标方程为
的极坐标方程为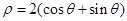 .
.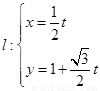 (
(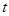 为参数)与曲线C交于
为参数)与曲线C交于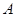 ,
,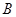 两点,与
两点,与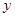 轴交于
轴交于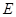 ,求
,求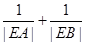 的值.
的值. 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线 的极坐标方程为
的极坐标方程为 .
. (
( 为参数)与曲线C交于
为参数)与曲线C交于 ,
, 两点,与
两点,与 轴交于
轴交于 ,求
,求 的值.
的值.