Question

已知直线l与抛物线y²=8x交于A，B两点，且l经过抛物线的焦点F；
（1）若已知A点的坐标为（8，8），求线段AB中点到准线的距离．
（2）求△ABO面积最小时，求直线l的方程．

Answer 1

分析：（1）确定抛物线的焦点坐标，求出AB的方程，代入抛物线方程，求得线段AB中点横坐标，即可求出线段AB中点到准线的距离．
（2）△ABO面积最小时，AB最短，此时AB⊥x轴，从而可求直线l的方程．

解答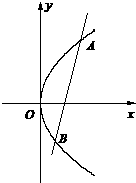：解：（1）依题意得F（2，0），∴直线AB方程为

y-0

8-0

=

x-2

8-2

，化简得y=

4

3

(x-2)，
代入y²=8x得2x²-17x+8=0，∴线段AB中点横坐标为

x1+x2

2

=

17 2

2

=

17

4

，
又准线方程为x=-2，∴中点到准线距离d=

17

4

-(-2)=

25

4

；
（2）设AB的方程为x=my+2，代入y²=8x，可得y²-8my-16=0，
设A（x₁，y₁），B（x₂，y₂），∴y₁+y₂=8m，y₁y₂=-16，
∴|y₁-y₂|=

64m2+64

，∴m=0时，|y₁-y₂|最小为8，
∵SABO=

1

2

•2|y₁-y₂|，∴m=0时，△ABO面积最小，此时AB⊥x轴，
∴面积最小为8，所求直线方程为：x=2．

点评：本题考查直线与抛物线的位置关系，考查三角形面积的计算，考查学生的计算能力，属于中档题．