题目内容
设函数
是定义在［-1,0）∪（0,1］上的偶函数,当x∈［-1,0）时, 
=x3-ax(a∈R).(1)当x∈（0,1］时,求
的解析式;
(2)若a＞3,试判断
在（0,1］上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈（0,1］时,
有最大值1.
分析：此题综合性较强,应注意知识间的相互联系和相互转化.
解：(1)∵x∈(0,1］时,-x∈［-1,0）,
∴=(-x)3-a(-x)=ax-x3.
又为偶函数,∴=,即=ax-x3.
(2)
=-3x2+a,∵x∈（0,1］,∴x2∈（0,1］.
∴-3x2≥-3.
∵a＞3,∴-3x2+a＞0,故
在（0,1］上为增函数.
(3)假设存在a,使得当x∈（0,1］时,
有最大值1.
∴
=a-3x2.
令
=0,∴-3x2+a=0,即a＞0时,x=±
.?
又∵x∈（0,1］,∴x=
且
＜1.
∴
在(0,
)上大于0,在(
,1)上小于0.
∴
=f(
)=
-
=
=1.
∴a=
时, 
有最大值1.
点评：关于存在性问题,处理的方法可以先假设存在,再寻找所得的结论.
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
是定义在［-1,0)∪(0,1］上的奇函数，当x∈［-1,0)时，
=2ax+
(a为实数).
在(0,1］上是增函数，求a的取值范围;
有最大值-6?
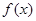是定义在［－1，0）∪（0，1］上的奇函数，当x∈［－1，0）时，
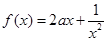（a∈R).
是定义在
上的函数，且
，当
时，
．
时，