题目内容
设函数 (1)若![]() 在(0,1]上是增函数,求a的取值范围;
在(0,1]上是增函数,求a的取值范围;
(2)是否存在a,使得当x∈(0,1]时,![]() 有最大值-6?
有最大值-6?
解析:(1)当x∈(0,1]时,-x∈[-1,0),?
∵![]() 在[-1,0)∪(0,1]上为奇函数,?
在[-1,0)∪(0,1]上为奇函数,?
∴![]() =-f(-x)=-(-2ax+
=-f(-x)=-(-2ax+![]() )=2ax-
)=2ax-![]() .?
.?
∵![]() 在(0,1]上是增函数,?
在(0,1]上是增函数,?
∴![]() =2a+
=2a+![]() >0在(0,1)上恒成立.?
>0在(0,1)上恒成立.?
∴a>-![]() 在(0,1)上恒成立.∴a≥-1.?
在(0,1)上恒成立.∴a≥-1.?
(2)当a≥-1时,![]() 在(0,1]上为增函数,?
在(0,1]上为增函数,?
∴![]() max=f(1)=2a-1=-6,a=-
max=f(1)=2a-1=-6,a=-![]() 不合题意.?
不合题意.?
当a<-1时,令f′(x)=0得x=-![]() .?
.?
当x∈(0,- ![]() )时,f′(x)>0,
)时,f′(x)>0, ![]() 为增函数;?
为增函数;?
当x∈(-![]() ,1]时,f′(x)<0,
,1]时,f′(x)<0, ![]() 为减函数.?
为减函数.?
∴![]() max=f(-
max=f(-![]() )=-2a
)=-2a![]() -
-![]() =-6.
=-6.
令![]() =t,则a=
=t,则a=![]() .∴-2
.∴-2![]() ·t-t2=-6.?
·t-t2=-6.?
∴t2=![]() ,即
,即![]() =
=![]() .∴a=-2
.∴a=-2![]() (a≤-1).
(a≤-1).

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
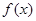 是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,
是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,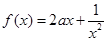 (a∈R).
(a∈R). 是定义在
是定义在 上的函数,且
上的函数,且 ,当
,当 时,
时, .
. 时,
时,