题目内容
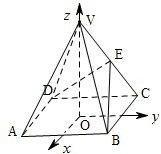 (2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.(Ⅰ)求cos<
| BE |
| DE |
(Ⅱ)记面BCV为α,面DCV为β,若∠BED是二面角α-VC-β的平面角,求cos∠BED的值.
分析:(I)确定向量的坐标,利用向量的夹角公式,即可求cos<
,
>;
(Ⅱ)确定h=
a,结合(I)的结论,即可求cos∠BED的值.
| BE |
| DE |
(Ⅱ)确定h=
| 2 |
解答: 解:(I)由题意知B(a,a,0),C(-a,a,0),D(-a,-a,0),
解:(I)由题意知B(a,a,0),C(-a,a,0),D(-a,-a,0),
E(-
,
,
),
由此得
=(-
,-
,
),
=(
,
,
),
∴
•
=(-
•
)+(-
•
)+
•
=-
+
,|
|=|
|=
=
.
由向量的数量积公式有cos<
,
>=
=
=
.
(II)若∠BED是二面角α-VC-β的平面角,则
⊥
,即有
•
=0.
又由C(-a,a,0),V(0,0,h),有
=(a,-a,h)且
=(-
,-
,
),
∴
•
=-
+
+
=0,即h=
a,
这时有cos<
,
>=
=
=-
.
∴cos∠BED=-
.
 解:(I)由题意知B(a,a,0),C(-a,a,0),D(-a,-a,0),
解:(I)由题意知B(a,a,0),C(-a,a,0),D(-a,-a,0),E(-
| a |
| 2 |
| a |
| 2 |
| h |
| 2 |
由此得
| BE |
| 3a |
| 2 |
| a |
| 2 |
| h |
| 2 |
| DE |
| a |
| 2 |
| 3a |
| 2 |
| h |
| 2 |
∴
| BE |
| DE |
| 3a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 3a |
| 2 |
| h |
| 2 |
| h |
| 2 |
| 3a2 |
| 2 |
| h2 |
| 4 |
| BE |
| DE |
(-
|
| 1 |
| 2 |
| 10a2+h2 |
由向量的数量积公式有cos<
| BE |
| DE |
| ||||
|
|
-
| ||||||||
|
| -6a2+h2 |
| 10a2+h2 |
(II)若∠BED是二面角α-VC-β的平面角,则
| BE |
| CV |
| BE |
| CV |
又由C(-a,a,0),V(0,0,h),有
| CV |
| BE |
| 3a |
| 2 |
| a |
| 2 |
| h |
| 2 |
∴
| BE |
| CV |
| 3a2 |
| 2 |
| a2 |
| 2 |
| h2 |
| 2 |
| 2 |
这时有cos<
| BE |
| DE |
| -6a2+h2 |
| 10a2+h2 |
-6a2+(
| ||
10a2+(
|
| 1 |
| 3 |
∴cos∠BED=-
| 1 |
| 3 |
点评:本小题主要考查空间直角坐标的概念、空间点和向量的坐标表示以及两个向量夹角的计算方法,考查运用向量研究空间图形的数学思想方法.

练习册系列答案
相关题目
 (2001•江西)某电厂冷却塔的外形是如图所示双曲线的一部分绕其中轴(即双曲线的虚轴)旋转所成的曲面,其中A、A′是双曲线的顶点,C、C′是冷却塔上口直径的两个端点,B、B′是下底直径的两个端点,已知AA′=14m,CC′=18m,BB′=22m,塔高20m.
(2001•江西)某电厂冷却塔的外形是如图所示双曲线的一部分绕其中轴(即双曲线的虚轴)旋转所成的曲面,其中A、A′是双曲线的顶点,C、C′是冷却塔上口直径的两个端点,B、B′是下底直径的两个端点,已知AA′=14m,CC′=18m,BB′=22m,塔高20m.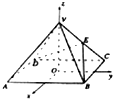 (2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.
(2001•江西)如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB.E为VC中点,正四棱锥底面边长为2a,高为h.