Question

（2001•江西）某电厂冷却塔的外形是如图所示双曲线的一部分绕其中轴（即双曲线的虚轴）旋转所成的曲面，其中A、A′是双曲线的顶点，C、C′是冷却塔上口直径的两个端点，B、B′是下底直径的两个端点，已知AA′=14m，CC′=18m，BB′=22m，塔高20m．
（Ⅰ）建立坐标系并写出该双曲线方程；
（Ⅱ）求冷却塔的容积（精确到10m³，塔壁厚度不计，π取3.14）．

Answer 1

分析：（I）建立直角坐标系xOy，AA′在x轴上，AA′的中点为坐标原点O，CC′与BB′平行于x轴，设出B、C的坐标，利用B、C在双曲线上，塔高20m，可得双曲线的标准方程；
（II）利用定积分知识，可求冷却塔的容积．

解答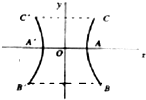：解：（I）如图建立直角坐标系xOy，AA′在x轴上，AA′的中点为坐标原点O，CC′与BB′平行于x轴．
设双曲线方程为

x2

a2

-

y2

b2

=1(a＞0，b＞0)，则a=

1

2

AA′=7．
又设B（11，y₁），C（9，y₂），
因为点B、C在双曲线上，所以有

112

72

-

y 2 1

b2

=1，①

92

72

-

y 2 2

b2

=1，②
由题意知y₂-y₁=20．③
由①、②、③得y1=-12，y2=8，b=7

2

．
故双曲线方程为

x2

49

-

y2

98

=1；
（II）由双曲线方程得x2=

1

2

y2+49．
设冷却塔的容积为V（m³），则V=π

∫

y2 y1

x2dy=π

∫

8 -12

(

1

2

y2+49)dy=π(

1

6

y3+49y)

|

8 -12

，
∴V≈4.25×10³（m³）．
答：冷却塔的容积为4.25×10³（m³）．

点评：本小题考查选择适当的坐标系建立曲线方程和解方程组等基础知识，考查应用所学积分知识、思想和方法解决实际问题的能力．