题目内容
如果2x2+1与4x2-2x-5互为相反数,则x的值为
1或-
| 2 |
| 3 |
1或-
.| 2 |
| 3 |
分析:根据2x2+1与4x2-2x-5互为相反数,得到关于x的一元二次方程,然后对方程进行因式分解,可得方程的因式分解形式,即可求解.
解答:解:∵2x2+1与4x2-2x-5互为相反数,
∴2x2+1+4x2-2x-5=0,即3x2-x-2=0,
∴(x-1)(3x+2)=0,
解得x1=1,x2=-
.
故答案为:1或-
.
∴2x2+1+4x2-2x-5=0,即3x2-x-2=0,
∴(x-1)(3x+2)=0,
解得x1=1,x2=-
| 2 |
| 3 |
故答案为:1或-
| 2 |
| 3 |
点评:本题考查了一元二次方程的解法,解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.注:互为相反数的两个数的和为0,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
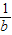 ,
,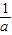 ),则称这两个不等式为对偶不等式.如果不等式x2-4
),则称这两个不等式为对偶不等式.如果不等式x2-4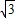 x•cosθ+2<0与不等式2x2-4x•sinθ+1<0为对偶不等式,且θ∈(
x•cosθ+2<0与不等式2x2-4x•sinθ+1<0为对偶不等式,且θ∈(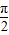 ,π),则θ= .
,π),则θ= . 在[-1,∞)上是减函数,则实数a的取值范围是(-8,-6];
在[-1,∞)上是减函数,则实数a的取值范围是(-8,-6];