题目内容
(本题满分16分)已知函数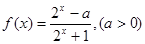 。
。
(Ⅰ)当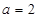 时,证明函数
时,证明函数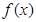 不是奇函数;
不是奇函数;
(Ⅱ)判断函数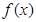 的单调性,并利用函数单调性的定义给出证明;
的单调性,并利用函数单调性的定义给出证明;
(Ⅲ)若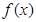 是奇函数,且
是奇函数,且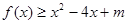 在
在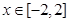 时恒成立,求实数
时恒成立,求实数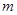 的取值范围。
的取值范围。
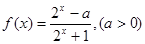 。
。(Ⅰ)当
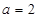 时,证明函数
时,证明函数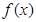 不是奇函数;
不是奇函数;(Ⅱ)判断函数
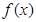 的单调性,并利用函数单调性的定义给出证明;
的单调性,并利用函数单调性的定义给出证明;(Ⅲ)若
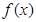 是奇函数,且
是奇函数,且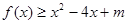 在
在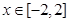 时恒成立,求实数
时恒成立,求实数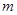 的取值范围。
的取值范围。(Ⅰ)当 时,
时, ,因为
,因为 ,
, ,
,
所以 ,故
,故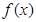 不是奇函数; ……………………………………4分
不是奇函数; ……………………………………4分
(Ⅱ)函数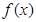 在
在 上为单调增函数, ………………………………………… 6分
上为单调增函数, ………………………………………… 6分
证明:设 ,则
,则 ……… 8分
……… 8分
∵ ,∴
,∴ ,
, ,且
,且
又∵ ,∴
,∴
∴ ,故
,故 。
。
∴函数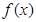 在
在 上为单调增函数。…………………………………………………10分
上为单调增函数。…………………………………………………10分
(Ⅲ)因为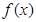 是奇函数,所以
是奇函数,所以 对任意
对任意 恒成立。
恒成立。
即 对任意
对任意 恒成立.
恒成立.
化简整理得 对任意
对任意 恒成立. ∴
恒成立. ∴ …………………12分
…………………12分
又因为 在
在 时恒成立,
时恒成立,
所以 在
在 时恒成立,
时恒成立,
令 ,设
,设 ,且
,且 ,
,
则
由(Ⅱ)可知, ,又
,又 ,
,
所以 ,即
,即 ,
,
故函数 在
在 上是增函数。………………………14分
上是增函数。………………………14分
所以 ,由
,由
 。
。
因此 的取值范围是
的取值范围是 。 ………………………………………………16分
。 ………………………………………………16分
 时,
时, ,因为
,因为 ,
, ,
,所以
 ,故
,故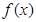 不是奇函数; ……………………………………4分
不是奇函数; ……………………………………4分(Ⅱ)函数
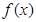 在
在 上为单调增函数, ………………………………………… 6分
上为单调增函数, ………………………………………… 6分证明:设
 ,则
,则 ……… 8分
……… 8分∵
 ,∴
,∴ ,
, ,且
,且
又∵
 ,∴
,∴
∴
 ,故
,故 。
。∴函数
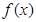 在
在 上为单调增函数。…………………………………………………10分
上为单调增函数。…………………………………………………10分(Ⅲ)因为
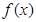 是奇函数,所以
是奇函数,所以 对任意
对任意 恒成立。
恒成立。即
 对任意
对任意 恒成立.
恒成立. 化简整理得
 对任意
对任意 恒成立. ∴
恒成立. ∴ …………………12分
…………………12分又因为
 在
在 时恒成立,
时恒成立,所以
 在
在 时恒成立,
时恒成立,令
 ,设
,设 ,且
,且 ,
,则

由(Ⅱ)可知,
 ,又
,又 ,
,所以
 ,即
,即 ,
,故函数
 在
在 上是增函数。………………………14分
上是增函数。………………………14分所以
 ,由
,由
 。
。因此
 的取值范围是
的取值范围是 。 ………………………………………………16分
。 ………………………………………………16分略

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 是定义在
是定义在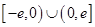 上的奇函数,当
上的奇函数,当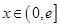 时,
时, 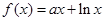 (其中e是自然界对数的底,
(其中e是自然界对数的底,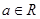 )
)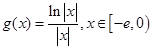 ,求证:当
,求证:当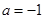 时,
时,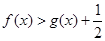 ;
;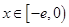 时,
时,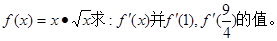
 的图象与
的图象与 轴相切于点
轴相切于点 ,
, 的极大值为m,
的极大值为m, .
. 在区间
在区间 上有最小值-2,求
上有最小值-2,求 的值。
的值。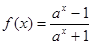 (
( 且
且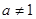 )
)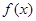 的定义域和值域
的定义域和值域 时,若对任意实数
时,若对任意实数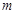 ,不等式
,不等式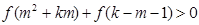 恒成立,求实数
恒成立,求实数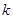 的取值范围
的取值范围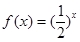 ,且
,且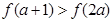 ,则实数
,则实数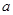 的取值范围是 。
的取值范围是 。 ,当
,当 时,有极大值
时,有极大值 。
。 的值; (2)求函数
的值; (2)求函数 的极小值。
的极小值。 ,
, 的最大值为
的最大值为