题目内容
已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)设![]() ,如果过点
,如果过点![]() 可作曲线
可作曲线![]() 的三条切线,证明:
的三条切线,证明:![]() .
.
(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
解析:
(1)求函数![]() 的导数;
的导数;![]() .
.
曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]() ,
,
即 ![]() .
.
(2)如果有一条切线过点![]() ,则存在
,则存在![]() ,使
,使![]() .
.
于是,若过点![]() 可作曲线
可作曲线![]() 的三条切线,则方程
的三条切线,则方程![]()
有三个相异的实数根.
记 ![]() ,则
,则 ![]()
![]() .
.
当![]() 变化时,
变化时,![]() 变化情况如下表:
变化情况如下表:
|
|
| 0 |
|
|
|
|
|
| 0 |
| 0 |
|
|
| 极大值 |
| 极小值 |
|
由![]() 的单调性,当极大值
的单调性,当极大值![]() 或极小值
或极小值![]() 时,方程
时,方程![]() 最多有一个实数根;
最多有一个实数根;
当![]() 时,解方程
时,解方程![]() 得
得![]() ,即方程
,即方程![]() 只有两个相异的实数根;
只有两个相异的实数根;
当![]() 时,解方程
时,解方程![]() 得
得![]() ,即方程
,即方程![]() 只有两个相异的实数根.
只有两个相异的实数根.
综上,如果过![]() 可作曲线
可作曲线![]() 三条切线,即
三条切线,即![]() 有三个相异的实数根,则
有三个相异的实数根,则![]()
即 ![]() .
.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 .
. 的定义域
;
的定义域
; ,求实数
,求实数 的值.
的值. .
. 在(0,+∞)上是减函数.
在(0,+∞)上是减函数.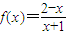 ;
; 成立,若存在求出x;若不存在,请说明理由.
成立,若存在求出x;若不存在,请说明理由. 令
令
 的定义域;
的定义域; 的奇偶性,并予以证明;
的奇偶性,并予以证明; ,猜想
,猜想 之间的关系并证明.
之间的关系并证明. ,
, 的定义域;(2)证明:
的定义域;(2)证明: ,求
,求 的取值范围。
的取值范围。