题目内容
已知函数f(x)=x2+2x+alnxa∈R.
①当a=-4时,求f(x)的最小值;
②若函数f(x)在区间(0,1)上为单调函数,求实数a的取值范围;
③当t≥1时,不等式f(2t-1)≥2f(t)-3恒成立,求实数a的取值范围.
解:①∵f(x)=x2+2x-4lnx(x>0)
∴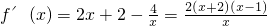 (2分)
(2分)
当x>1时,f'(x)>0,当0<x<1时,f'(x)<0
∴f(x)在(0,1)上单调减,在(1,+∞)上单调增
∴f(x)min=f(1)=3(4分)
②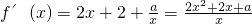 (5分)
(5分)
若f(x)在(0,1)上单调增,则2x2+2x+a≥0在x∈(0,1)上恒成立?a≥-2x2-2x恒成立
令u=-2x2-2x,x∈(0,1),则 ,umax=0
,umax=0
∴a≥0(7分)
若f(x)在(0,1)上单调减,则2x2+2x+a≤0在x∈(0,1)上恒成立?a≤[-2x2-2x]min=-4
综上,a的取值范围是:(-∞,-4]∪[0,+∞)(9分)
③(2t-1)2+2(2t-1)+aln(2t-1)≥2t2+4t+2alnt-3恒成立a[ln(2t-1)-2lnt]≥-2t2+4t-2?a[ln(2t-1)-lnt2]≥2[(2t-1)-t2](10分)
当t=1时,不等式显然成立
当t>1时,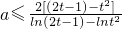 在t>1时恒成立(11分)
在t>1时恒成立(11分)
令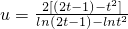 ,即求u的最小值
,即求u的最小值
设A(t2,lnt2),B(2t-1,ln(2t-1)),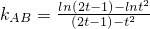 ,
,
且A、B两点在y=lnx的图象上,又∵t2>1,2t-1>1,故0<kAB<y'|x=1=1
∴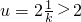 ,故a≤2
,故a≤2
即实数a的取值范围为(-∞,2](14分)
分析:①先求出其导函数,得到其在定义域上的单调性即可求出f(x)的最小值;
②先求出其导函数,把f(x)在(0,1)上单调增转化为2x2+2x+a≥0在x∈(0,1)上恒成立?a≥-2x2-2x恒成立,再利用二次函数在固定区间上求最值的方法求出-2x2-2x的最大值即可求实数a的取值范围;
③根据(2t-1)2+2(2t-1)+aln(2t-1)≥2t2+4t+2alnt-3恒成立则a[ln(2t-1)-2lnt]≥-2t2+4t-2?a[ln(2t-1)-lnt2]≥2[(2t-1)-t2再讨论他的取值范围
点评:该题考查函数的求导,利用导数求函数的单调性,利用恒等式求函数的最值问题,注意不要掉了自变量的取值范围.
∴
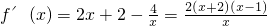 (2分)
(2分)当x>1时,f'(x)>0,当0<x<1时,f'(x)<0
∴f(x)在(0,1)上单调减,在(1,+∞)上单调增
∴f(x)min=f(1)=3(4分)
②
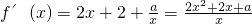 (5分)
(5分)若f(x)在(0,1)上单调增,则2x2+2x+a≥0在x∈(0,1)上恒成立?a≥-2x2-2x恒成立
令u=-2x2-2x,x∈(0,1),则
 ,umax=0
,umax=0∴a≥0(7分)
若f(x)在(0,1)上单调减,则2x2+2x+a≤0在x∈(0,1)上恒成立?a≤[-2x2-2x]min=-4
综上,a的取值范围是:(-∞,-4]∪[0,+∞)(9分)
③(2t-1)2+2(2t-1)+aln(2t-1)≥2t2+4t+2alnt-3恒成立a[ln(2t-1)-2lnt]≥-2t2+4t-2?a[ln(2t-1)-lnt2]≥2[(2t-1)-t2](10分)
当t=1时,不等式显然成立
当t>1时,
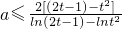 在t>1时恒成立(11分)
在t>1时恒成立(11分)令
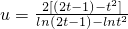 ,即求u的最小值
,即求u的最小值设A(t2,lnt2),B(2t-1,ln(2t-1)),
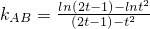 ,
,且A、B两点在y=lnx的图象上,又∵t2>1,2t-1>1,故0<kAB<y'|x=1=1
∴
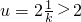 ,故a≤2
,故a≤2即实数a的取值范围为(-∞,2](14分)
分析:①先求出其导函数,得到其在定义域上的单调性即可求出f(x)的最小值;
②先求出其导函数,把f(x)在(0,1)上单调增转化为2x2+2x+a≥0在x∈(0,1)上恒成立?a≥-2x2-2x恒成立,再利用二次函数在固定区间上求最值的方法求出-2x2-2x的最大值即可求实数a的取值范围;
③根据(2t-1)2+2(2t-1)+aln(2t-1)≥2t2+4t+2alnt-3恒成立则a[ln(2t-1)-2lnt]≥-2t2+4t-2?a[ln(2t-1)-lnt2]≥2[(2t-1)-t2再讨论他的取值范围
点评:该题考查函数的求导,利用导数求函数的单调性,利用恒等式求函数的最值问题,注意不要掉了自变量的取值范围.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|