题目内容
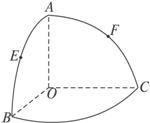
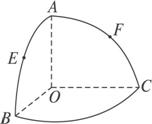
如图O为半径为1的球心,点A、B、C在球面上,OA,OB,OC两两垂直,E,F分别是大圆弧AB与AC中点,则点E、F在该球面上的球面距离为 .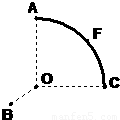
【答案】分析:欲求点E、F在该球面上的球面距离,关键是求出球心角.过E、F做AO的垂面交AO于G,求出EG,EF,然后求出∠EOF,利用扇形弧长公式求球面距离即可.
解答: 解:作EG⊥OA于点G,连EG、EF、FG,如图,
解:作EG⊥OA于点G,连EG、EF、FG,如图,

∴ (5分)
(5分)
∴ ,
,
∴E、F,在该球面上的球面距离为 (7分)
(7分)
故答案为: .
.
点评:本小题主要考查扇线面位置关系、形弧长公式、球面距离及相关计算等基础知识,考查空间想象力,属于基础题.
解答:
 解:作EG⊥OA于点G,连EG、EF、FG,如图,
解:作EG⊥OA于点G,连EG、EF、FG,如图,
∴
 (5分)
(5分)∴
 ,
,∴E、F,在该球面上的球面距离为
 (7分)
(7分)故答案为:
 .
.点评:本小题主要考查扇线面位置关系、形弧长公式、球面距离及相关计算等基础知识,考查空间想象力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图O为半径为1的球心,点A、B、C在球面上,OA,OB,OC两两垂直,E,F分别是大圆弧AB与AC中点,则点E、F在该球面上的球面距离为
如图O为半径为1的球心,点A、B、C在球面上,OA,OB,OC两两垂直,E,F分别是大圆弧AB与AC中点,则点E、F在该球面上的球面距离为