题目内容

非零向量
OA
=a，
OB
=b若点B关于
OA
所在直线的对称点为B1，则向量
OB
+
OB1
为（　　）
A、
2(a•b)a
|a|2
B、
(a•b)a
|a|2
C、
2(a•b)a
|a|
D、
(a•b)a
|a|
分析：容易知道，由平行四边形法则向量
OB
+
OB1
的方向与向量
OA
的方向相同，因此只需要求得与向量
OA
方向相同的单位向量
a
|
a
|
以及向量
OB
在向量
OA
方向上的投影
a
•
b
|
a
|
，即可得到向量
OB
+
OB1
．
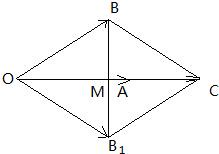解答：精英家教网解：如图由题意点B关于
OA
所在直线的对称点为B1，
所以∠BOA=∠B1OA，
所以又由平行四边形法则知：
OB
+
OB1
=
OC
，
且向量
OC
的方向与向量
OA
的方向相同，
由数量积的概念，向量
OB
在向量
OA
方向上的投影是OM=
a
•
b
|
a
|
，
又设与向量
OA
方向相同的单位向量为：
a
|
a
|
，
所以向量
OC
=2
OM
=2•
a
•
b
|
a
|
•
a
|
a
|
=
2(
a
•
b
)
a
 
|
a
|2

故应选：A
点评：本题考查向量加法的平行四边形法则，向量的数量积的概念，向量的模的概念．
练习册系列答案
相关题目
已知非零向量
OA
，
OB
，
OC
满足：
OA
=a
OB
+β
OC
（a，β∈R），给出下列命题：
①若a=
3
2
，β=-
1
2
，则A、B、C三点共线；
②若a＞0，β＞0，|
OA
|=
3
，|
OB
|=|
OC
|=1，＜
OB
，
OC
＞=
2π
3
，＜
OA
，
OB
＞=
π
2
则a+β=3；
③已知等差数列{an}中，an＞an+1＞0（n∈N*），a2=a，a2009=β若A、B、C三点共线，但O点 不在直线BC上，则
1
a3
+
4
a2008
的最小值为9；
④若β≠0，且A、B、C三点共线，则A分
BC
所在的比λ一定为
a
β
．
其中你认为正确的所有命题的序号是
①②③④
①②③④
．
（2010•青岛一模）在数列{an}中，an+1=an+a（n∈N*，a为常数），若平面上的三个不共线的非零向量
OA
，
OB
，
OC
满足
OC
=a1
OA
+a2010
OB
，三点A，B，C共线且该直线不过O点，则S2010等于（　　）
（2010•宿州三模）在数列{an}中，已知an+1+an-1=2an（n∈N+，n≥2），若平面上的三个不共线的非零向量
OA
、
OB
、
OC
，满足
OC
=a1005
OA
+a1006
OB
，三点A、B、C共线，且直线不过O点，则S2010等于（　　）
在数列{an}中，an+1=an+a（n∈N*，a为常数），若不共线的非零向量
OA
，
OB
，
OC
满足
OC
=a1
OA
+a2010
OB
，三点A，B，C共线且该直线不过O点，则S2010等于
1005
1005
．
已知A，B是抛物线x2=2py（p＞0）上的两个动点，O为坐标原点，非零向量
OA
， 
OB
满足|
OA
+
OB
|=|
OA
-
OB
|．
（Ⅰ）求证：直线AB经过一定点；
（Ⅱ）当AB的中点到直线y-2x=0的距离的最小值为
2
5
5
时，求p的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网