题目内容
如图,在锥体P-ABCD中,ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=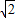 ,PB=2,E,F分别是BC,PC的中点
,PB=2,E,F分别是BC,PC的中点(1)证明:AD⊥平面DEF
(2)求二面角P-AD-B的余弦值.
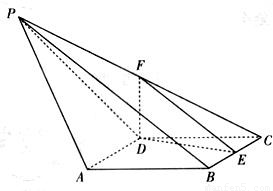
【答案】分析:(1)利用线面垂直的判定定理进行证明是解决本题的关键,在平面DEF中找两条相交直线与AD垂直,利用60°角菱形的特征可以发现AD⊥DE,通过取出AD的中点构造一个平面可以证明AD⊥EF;
(2)利用(1)中的结论找到二面角P-AD-B的平面角是解决本题的关键,求角往往要利用三角形中的余弦定理.
解答:解:(1)取AD的中点G,连接PG,BG,在△ABG中,根据余弦定理可以算出BG=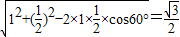 ,
,
发现AG2+BG2=AB2,可以得出AD⊥BG,又DE∥BG
∴DE⊥AD,
又PA=PD,可以得出AD⊥PG,而PG∩BG=G,
∴AD⊥平面PBG,而PB?平面PBG,
∴AD⊥PB,又PB∥EF,
∴AD⊥EF.又EF∩DE=E,∴AD⊥平面DEF.
(2)由(1)知,AD⊥平面PBG,所以∠PGB为二面角P-AD-B的平面角,在△PBG中,PG=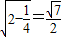 ,BG=
,BG=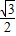 ,PB=2,由余弦定理得
,PB=2,由余弦定理得
cos∠PGB=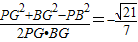 ,因此二面角P-AD-B的余弦值为
,因此二面角P-AD-B的余弦值为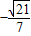 .
.
点评:本题考查立体几何中基本的线面关系,考查线面垂直的判定方法,考查二面角的求法,训练了学生基本的空间想象能力,考查学生的转化与化归思想,解三角形的基本知识和学生的运算能力,属于基本的立体几何题.
(2)利用(1)中的结论找到二面角P-AD-B的平面角是解决本题的关键,求角往往要利用三角形中的余弦定理.
解答:解:(1)取AD的中点G,连接PG,BG,在△ABG中,根据余弦定理可以算出BG=
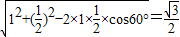 ,
,发现AG2+BG2=AB2,可以得出AD⊥BG,又DE∥BG
∴DE⊥AD,
又PA=PD,可以得出AD⊥PG,而PG∩BG=G,
∴AD⊥平面PBG,而PB?平面PBG,
∴AD⊥PB,又PB∥EF,
∴AD⊥EF.又EF∩DE=E,∴AD⊥平面DEF.
(2)由(1)知,AD⊥平面PBG,所以∠PGB为二面角P-AD-B的平面角,在△PBG中,PG=
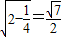 ,BG=
,BG=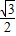 ,PB=2,由余弦定理得
,PB=2,由余弦定理得cos∠PGB=
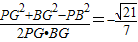 ,因此二面角P-AD-B的余弦值为
,因此二面角P-AD-B的余弦值为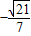 .
.点评:本题考查立体几何中基本的线面关系,考查线面垂直的判定方法,考查二面角的求法,训练了学生基本的空间想象能力,考查学生的转化与化归思想,解三角形的基本知识和学生的运算能力,属于基本的立体几何题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 (2013•四川)如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1=2,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
(2013•四川)如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1=2,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.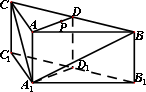
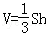 ,其中S为底面面积,h为高)
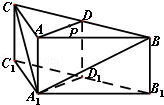
,其中S为底面面积,h为高)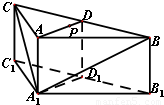 如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1=2,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点.
如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1=2,∠BAC=120°,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点. ,其中S为底面面积,h为高)
,其中S为底面面积,h为高)