Question

（12分）如图，在三棱柱ABC﹣A₁B₁C中，侧棱AA₁⊥底面ABC，AB=AC=2AA₁=2，∠BAC=120°，D，D₁分别是线段BC，B₁C₁的中点，P是线段AD上异于端点的点．

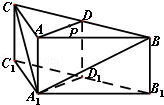
（Ⅰ）在平面ABC内，试作出过点P与平面A₁BC平行的直线l，说明理由，并证明直线l⊥平面ADD₁A₁；

（Ⅱ）设（Ⅰ）中的直线l交AC于点Q，求三棱锥A₁﹣QC₁D的体积．（锥体体积公式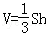：，其中S为底面面积，h为高）

 

Answer 1

【答案】

（Ⅰ）见解析（Ⅱ）

【解析】（Ⅰ）在平面ABC内，过点P作直线l和BC平行，由于直线l不在平面A₁BC内，而BC在平面A₁BC内，

故直线l与平面A₁BC平行．

三角形ABC中，∵AB=AC=2AA₁=2，∠BAC=120°，D，D₁分别是线段BC，B₁C₁的中点，∴AD⊥BC，∴l⊥AD．

再由AA₁⊥底面ABC，可得 AA₁⊥l．

而AA₁∩AD=A，

∴直线l⊥平面ADD₁A₁ ．

（Ⅱ）设（Ⅰ）中的直线l交AC于点Q，过点D作DE⊥AC，

∵侧棱AA₁⊥底面ABC，故三棱柱ABC﹣A₁B₁C为直三棱柱，

故DE⊥平面AA₁C₁C．

直角三角形ACD中，∵AC=2，∠CAD=60°，∴AD=AC•cos60°=1，∴DE=AD•sin60°=．

∵===1，

∴三棱锥A₁﹣QC₁D的体积 ==••DE=×1×=．