题目内容
已知△ABC的面积S满足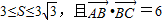 ,
,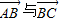 的夹角为θ.
的夹角为θ.(Ⅰ)求θ的取值范围;
(Ⅱ)求函数f(θ)=sin2θ+2sinθcosθ+3cos2θ的最大值.
【答案】分析:(Ⅰ)利用向量的数量积、三角形的面积公式和正切函数的单调性即可求出;
(Ⅱ)利用三角恒等变形及三角函数的单调性即可求出.
解答:解:(I)由题意知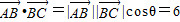 .
.
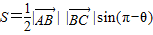 =
=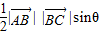
=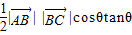
=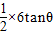 =3tanθ.
=3tanθ.
∵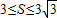 ,
,
∴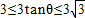 ,∴
,∴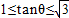 .
.
又∵θ∈[0,π],∴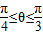 .
.
(II)∵f(θ)=sin2θ+2sinθcosθ+3cos2θ
=1+sin2θ+2cos2θ
=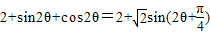 .
.
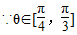 ,∴
,∴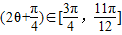 .
.
∵y=sinx在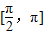 上单调递减,
上单调递减,
∴当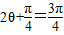 ,即
,即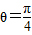 时,
时,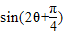 取得最大值
取得最大值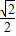 ,
,
∴f(θ)的最大值为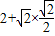 =3.
=3.
点评:熟练掌握向量的数量积运算和三角函数的单调性是解题的关键.
(Ⅱ)利用三角恒等变形及三角函数的单调性即可求出.
解答:解:(I)由题意知
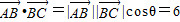 .
.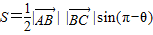 =
=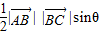
=
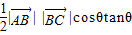
=
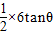 =3tanθ.
=3tanθ.∵
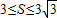 ,
,∴
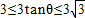 ,∴
,∴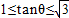 .
.又∵θ∈[0,π],∴
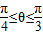 .
.(II)∵f(θ)=sin2θ+2sinθcosθ+3cos2θ
=1+sin2θ+2cos2θ
=
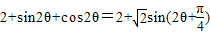 .
.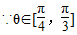 ,∴
,∴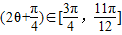 .
.∵y=sinx在
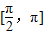 上单调递减,
上单调递减,∴当
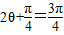 ,即
,即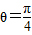 时,
时,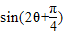 取得最大值
取得最大值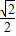 ,
,∴f(θ)的最大值为
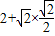 =3.
=3.点评:熟练掌握向量的数量积运算和三角函数的单调性是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目