题目内容
已定义在 上的偶函数
上的偶函数 满足
满足 时,
时, 成立,若
成立,若 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
C
解析试题分析:构造函数 ,由函数
,由函数 是R上的偶函数,函数
是R上的偶函数,函数 是R上的奇函数可得
是R上的奇函数可得 是R上的奇函数,又当
是R上的奇函数,又当 时
时 ,所以函数
,所以函数 在
在 时的单调性为单调递减函数;所以
时的单调性为单调递减函数;所以 在
在 时的单调性为单调递减函数,因为
时的单调性为单调递减函数,因为 ,
,  ,
, ,故
,故 ,即:
,即: ,故选C.
,故选C.
考点:函数奇偶性的性质,简单复合函数的导数,函数的单调性与导数的关系.

练习册系列答案
相关题目
同时满足以下三个条件的函数是( )
①图像过点 ;②在区间
;②在区间 上单调递减③是偶函数 .
上单调递减③是偶函数 .
A. | B. |
C.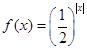 | D.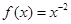 |
设函数f(x)=x2+mx(m∈R),则下列命题中的真命题是( )
| A.任意m∈R,使y=f(x)都是奇函数 | B.存在m∈R,使y=f(x)是奇函数 |
| C.任意m∈R,使y=f(x)都是偶函数 | D.存在m∈R,使y=f(x)是偶函数 |
设 ,
, 是二次函数,若
是二次函数,若 的值域是
的值域是 ,则
,则 的值域是( )
的值域是( )
A. | B. |
C. | D. |
如果 ,则当
,则当 时,
时, ( )
( )
A. | B. | C. | D. |
函数 的单调递增区间为( )
的单调递增区间为( )
A. | B. | C. | D. |
下列函数,在其定义域内既是奇函数又是增函数的是( )
A.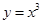 | B.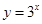 | C.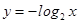 | D.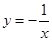 |
函数 的零点所在的一个区间是( )
的零点所在的一个区间是( )
A. | B. | C. | D.(1,2) |
函数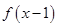 是
是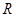 上的奇函数,
上的奇函数,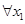 、
、 ,
,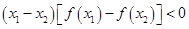 ,则
,则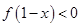 的解集是( )
的解集是( )
A.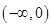 | B.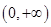 | C.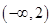 | D.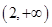 |