题目内容
设函数f(x)=x2+mx(m∈R),则下列命题中的真命题是( )
| A.任意m∈R,使y=f(x)都是奇函数 | B.存在m∈R,使y=f(x)是奇函数 |
| C.任意m∈R,使y=f(x)都是偶函数 | D.存在m∈R,使y=f(x)是偶函数 |
D
解析试题分析:函数 首先是二次函数,不可能是奇函数,当
首先是二次函数,不可能是奇函数,当 时,它是偶函数,当
时,它是偶函数,当 时,它也不是偶函数.故选D.
时,它也不是偶函数.故选D.
考点:函数的奇偶性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
规定 ,则函数
,则函数 的值域为
的值域为
A. | B. | C. | D. |
已知函数 的定义域为
的定义域为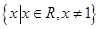 ,且
,且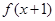 为奇函数,当
为奇函数,当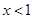 时,
时,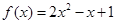 ,那么当
,那么当 时,
时, 的递减区间是( )
的递减区间是( )
A.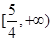 | B. | C.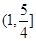 | D.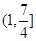 |
已知函数 为奇函数,且当
为奇函数,且当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
若函数 ,则函数
,则函数 ( )
( )
A.是奇函数,在 是增函数 是增函数 | B.是偶函数,在 是减函数 是减函数 |
C.是偶函数,在 是增函数 是增函数 | D.是奇函数,在 是减函数 是减函数 |
如图给出了函数 ,
, ,
, ,
, 的图像,则与函数
的图像,则与函数 ,
, ,
, ,
, 依次对应的图像是( )
依次对应的图像是( ) 
| A.①②③④ | B.①③②④ |
| C.②③①④ | D.①④③② |
若函数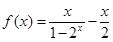 ,则函数
,则函数 ( )
( )
A.是偶函数,在 是增函数 是增函数 | B.是偶函数,在 是减函数 是减函数 |
C.是奇函数,在 是增函数 是增函数 | D.是奇函数,在 是减函数 是减函数 |
已定义在 上的偶函数
上的偶函数 满足
满足 时,
时, 成立,若
成立,若 ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
已知 为偶函数,且
为偶函数,且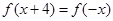 ,当
,当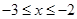 时,
时,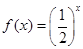 ,则
,则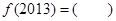
A.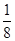 | B. | C.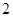 | D.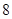 |