题目内容
在等腰直角三角形ABC中,直角顶点为C.(1)在斜边AB上任取一点M,求AM<AC的概率;
(2)在△ACB的内部,以C为端点任作一条射线CM,与线段AB交于点M,求AM<AC的概率.
【答案】分析:(1)欲求AM<AC的概率,先求出M点可能在的位置的长度,AC的长度,再让两者相除可得答案;
(2)由于过直角顶点C在∠ACB内部任作一射线CM,故可以认为所有可能结果的区域为∠ACB,可将事件A构成的区域为∠ACC',以角度为“测度”加以计算,可得本题答案.
解答:解:(1)在等腰直角三角形ABC中,设AC长为1,则AB长为 ,
,
在AB上取点D,使AD=1,则若M点在线段AB上,满足条件.
∵AD=1,AB= ,
,
∴AM<AC的概率为P1= =
= .
.
(2)在AB上取AC'=AC,则∠ACC′= =67.5°.
=67.5°.
则所有可能结果的区域为∠ACB,事件A构成的区域为∠ACC'.
∵∠ACB=90°,∠ACC'=67.5°.
∴AM<AC的概率为P2= =
= .
.
答:(1)在斜边AB上任取一点M,则AM<AC的概率是 ;
;
(2)在∠ACB的内部,以C为端点任作一条射线CM,与线段AB交于点M,则AM<AC的概率为 .
.
点评:本题给出等腰Rt△ABC,求在两种取法下使得AM<AC的概率.着重考查了几何概型及其应用的知识,属于中档题.解题时注意题意中的“测度”,准确把握“测度”是解决问题的关键.
(2)由于过直角顶点C在∠ACB内部任作一射线CM,故可以认为所有可能结果的区域为∠ACB,可将事件A构成的区域为∠ACC',以角度为“测度”加以计算,可得本题答案.
解答:解:(1)在等腰直角三角形ABC中,设AC长为1,则AB长为
 ,
,
在AB上取点D,使AD=1,则若M点在线段AB上,满足条件.
∵AD=1,AB=
 ,
,∴AM<AC的概率为P1=
 =
= .
.(2)在AB上取AC'=AC,则∠ACC′=
 =67.5°.
=67.5°.则所有可能结果的区域为∠ACB,事件A构成的区域为∠ACC'.
∵∠ACB=90°,∠ACC'=67.5°.
∴AM<AC的概率为P2=
 =
= .
.答:(1)在斜边AB上任取一点M,则AM<AC的概率是
 ;
;(2)在∠ACB的内部,以C为端点任作一条射线CM,与线段AB交于点M,则AM<AC的概率为
 .
.点评:本题给出等腰Rt△ABC,求在两种取法下使得AM<AC的概率.着重考查了几何概型及其应用的知识,属于中档题.解题时注意题意中的“测度”,准确把握“测度”是解决问题的关键.

练习册系列答案
相关题目
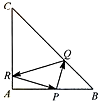 在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到点P(如图).若光线QR经过△ABC的重心(三角形三条中线的交点),则AP=
在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到点P(如图).若光线QR经过△ABC的重心(三角形三条中线的交点),则AP=