Question

在正方体的8个顶点中任取2个顶点所得的所有直线中任取2条，则所取的2条成一对异面直线的概率为（ ）
A．
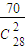
B．
C．
D．

Answer 1

【答案】分析：根据题意，首先由正方体的结构特征，可得从正方体的8个顶点中任取2个顶点，可以确定28条直线，再由组合数公式可得一共可以得到有C₂₈²组直线，进而分类讨论其中直线异面的情况，可得异面直线的组数，由等可能事件的概率公式，计算可得答案．
解答：解：从正方体的8个顶点中任取2个顶点，有C₈²=28种取法，即可以确定28条直线，
从这28条直线中，任取2条，有C₂₈²种取法，即可以确定C₂₈²组直线，
其中异面的情况有：
①、棱与棱异面：每条棱有4条棱与其异面，共有情况×12×4=24组，
②、棱与面对角线异面：每条棱有6条面对角线与其异面，共有情况12×6=72组，
③、棱与体对角线异面：每条棱有2条面对角线与其异面，共有情况12×2=24组，
④、面对角线与面对角线异面：每条面对角线与5条面对角线异面，共有情况×12×5=30组，
⑤、面对角线与体对角线异面：每条面对角线与2条面对角线异面，共有情况12×2=24组，
则异面直线的组数为24+72+24+30+24=174组，
所取的2条成一对异面直线的概率为；
故选D．
点评：本题考查等可能事件的概率计算与正方体的结构特征，涉及异面直线的判断方法，难点是分类讨论，确定异面直线的组数．