题目内容
已知数列 中,其中
中,其中 为数列
为数列 的前
的前 项和,并且
项和,并且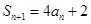 (
( ,
, .
.
(1)设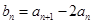 (
( ),求证:数列
),求证:数列 是等比数列;
是等比数列;
(2)设数列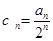 (
( ),求证:数列
),求证:数列 是等差数列;
是等差数列;
(3)求数列 的通项公式和前
的通项公式和前 项.
项.
(1)详见解析;(2)详见解析;(3)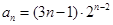 ,
, .
.
解析试题分析:(1)首先条件中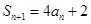 如何处理,通常要归一,即一是转化为相邻三项的关系;二是转化为和之间的关系,这里是转化为相邻三项的关系,接下来根据等比数列的定义,易得数列
如何处理,通常要归一,即一是转化为相邻三项的关系;二是转化为和之间的关系,这里是转化为相邻三项的关系,接下来根据等比数列的定义,易得数列 是等比数列;(2)根据等差数列的定义,结合(1)不难证明数列
是等比数列;(2)根据等差数列的定义,结合(1)不难证明数列 是等比数列;(3)有了(1)(2)的铺垫很容易求得数列
是等比数列;(3)有了(1)(2)的铺垫很容易求得数列 的通项公式,对照通项公式的特点:它是由一个等差数列与一个等比数列对应项相乘得到的,故用错位相减法求数列
的通项公式,对照通项公式的特点:它是由一个等差数列与一个等比数列对应项相乘得到的,故用错位相减法求数列 的
的 .
.
试题解析:(1)证明: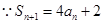 ,
,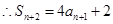 ,两式相减得
,两式相减得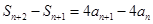 --3分
--3分
即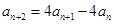 ,变形得
,变形得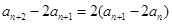
设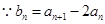 ,则有
,则有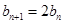 (
( ),又
),又 ,
,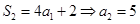 ,
,
从而 ,由此可知,数列
,由此可知,数列 是公比为2的等比数列.
是公比为2的等比数列.
(2)证明:由(1)知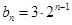
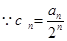 ,
,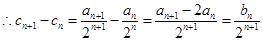
将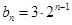 代入得
代入得 (
( )
)
由此可知,数列 是公差为
是公差为 ,首项
,首项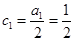 的等差数列,
的等差数列,
故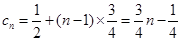 (
( ).
).
(3)由(2)可知: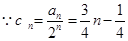 ,
,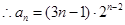
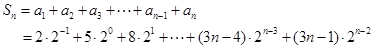
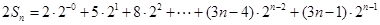
两式错位相减: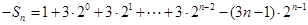
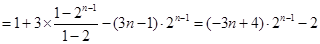
所以
考点:数列中的递推关系式处理及转化数学思想的使用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
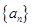 中,
中,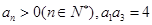 ,且
,且 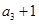 是
是  和
和 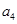 的等差中项,若
的等差中项,若 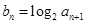
 的通项公式;
的通项公式; 满足
满足 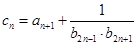 ,求数列
,求数列 }中,
}中, =14,前10项和
=14,前10项和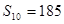 .
.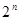 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前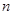 项和
项和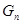 .
. 满足:
满足: ,
,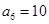 .
.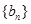 的各项均为正数,
的各项均为正数,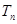 为其前
为其前 项和,若
项和,若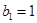 ,
,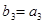 ,求
,求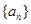 的首项为23,公差为整数,且第6项为正数,从第7项起为负数。
的首项为23,公差为整数,且第6项为正数,从第7项起为负数。 是正数时,求n的最大值。
是正数时,求n的最大值。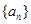 为等差数列,
为等差数列,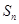 为其前
为其前 项和,若
项和,若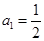 ,
,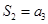 ,则
,则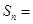 ___________.
___________. 共有
共有 项,所有奇数项之和为
项,所有奇数项之和为 ,所有偶数项之和为
,所有偶数项之和为 ,则n等于____________.
,则n等于____________.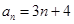 ,则数列{an}是公差为 的等差数列.
,则数列{an}是公差为 的等差数列.