题目内容
抛物线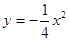 的焦点坐标是:
的焦点坐标是:
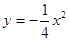 的焦点坐标是:
的焦点坐标是:| A.(0,-1) | B.(0,1) | C.(1,0) ( | D.(-1,0) |
A
分析:把抛物线y="-"
 x2的方程化为标准方程,求出 p值和开口方向,从而写出焦点坐标.
x2的方程化为标准方程,求出 p值和开口方向,从而写出焦点坐标.解:抛物线y=-
 x2的标准方程为 x2=-4y,开口向下,
x2的标准方程为 x2=-4y,开口向下,p=2,
 =1,故焦点为(0,-1),
=1,故焦点为(0,-1),故选 A.

练习册系列答案
相关题目
题目内容
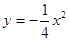 的焦点坐标是:
的焦点坐标是:| A.(0,-1) | B.(0,1) | C.(1,0) ( | D.(-1,0) |
 x2的方程化为标准方程,求出 p值和开口方向,从而写出焦点坐标.
x2的方程化为标准方程,求出 p值和开口方向,从而写出焦点坐标. x2的标准方程为 x2=-4y,开口向下,
x2的标准方程为 x2=-4y,开口向下, =1,故焦点为(0,-1),
=1,故焦点为(0,-1),