Question

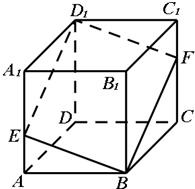如图，正方体ABCD-A₁B₁C₁D₁的棱长为1，E，F分别在棱AA₁和CC₁上（含线段端点）．
（1）如果AE=C₁F，试证明B，E，D₁，F四点共面；
（2）在（1）的条件下，是否存在一点E，使得直线A₁B和平面BFE所成角等于

π

6

？如果存在，确定E的位置；如果不存在，试说明理由．

Answer 1

分析：（1）正方体ABCD-A₁B₁C₁D₁的中，由AE=C₁F容易证明得D₁F=BE，D₁F∥BE，B，E，D₁，F四点共面；
（2）过点A₁作A₁O⊥平面ABC₁垂足为O，则∠A₁BO即为A₁B与平面ABC₁所成的角，由等体积法可求A₁O，在Rt△A₁BO中sin∠A1BO=

A1O

AB

=

1

2

可得∠A1BO=

π

6

，所以可求得当与A重合时满足条件

解答：证明：（1）正方体ABCD-A₁B₁C₁D₁的中，由AE=C₁F可得△AEB≌△D₁C₁F，从而可得D₁F=BE，由等角定理可得D₁F∥BE四边形BED₁F为平行四边形故，B，E，D₁，F四点共面；
（2）假设存在满足条件的点E
过点A₁作A₁O⊥平面ABC₁垂足为O，则∠A₁BO即为A₁B与平面ABC₁所成的角
由VA1- ABC1=VC1- ABA1可得A1O=

1 3 ×S△ABA1×1

1 3 ×S△ABC1

=

2

2

在Rt△A₁BO中sin∠A1BO=

A1O

AB

=

2 2

2

=

1

2

∴∠A1BO=

π

6

当E与A重合时满足条件

点评：等体积法求解锥体的高是高考在立体几何部分的考查热点和重点，出现的频率比较高，线面角的求解的关键是先要寻求线面垂足，进而找出角，然后在直角三角形中求解出角．