题目内容
已知a,x∈R,A={2,4,x2-5x+9},B={3,x2+ax+a}.求:
(1)使A={2,3,4}的x值;
(2)使2∈B,B?A的a,x的值.
(1)使A={2,3,4}的x值;
(2)使2∈B,B?A的a,x的值.
分析:(1)由已知A={2,4,x2-5x+9},A={2,3,4},根据集合相等可得x2-5x+9=3,解出即可;
(2)由2∈B,B?A,利用元素与集合之间的属于关系、集合之间的包含关系可得x2+ax+a=2且x2-5x+9=3,联立解出即可.
(2)由2∈B,B?A,利用元素与集合之间的属于关系、集合之间的包含关系可得x2+ax+a=2且x2-5x+9=3,联立解出即可.
解答:解:(1)∵A={2,4,x2-5x+9},A={2,3,4},
∴x2-5x+9=3,化为x2-5x+6=0,
解得x=2或3.
(2)∵2∈B,B?A,
∴x2+ax+a=2且x2-5x+9=3,
由x2-5x+9=3,化为x2-5x+6=0,解得x=2或3.
当x=2时,22+2a+a=2,解得a=-
;
当x=3时,32+3a+a=2,解得a=-
.
∴x2-5x+9=3,化为x2-5x+6=0,
解得x=2或3.
(2)∵2∈B,B?A,
∴x2+ax+a=2且x2-5x+9=3,
由x2-5x+9=3,化为x2-5x+6=0,解得x=2或3.
当x=2时,22+2a+a=2,解得a=-
| 2 |
| 3 |
当x=3时,32+3a+a=2,解得a=-
| 7 |
| 4 |
点评:本题综合考查了元素与集合之间的属于关系、集合之间的基本关系、一元二次方程的解法等基础知识,正确理解是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由. ,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间
,设g(x)是函数f(x)在区间[0,+∞)上的导函数,问是否存在实数a,满足a>1并且使g(x)在区间 上的值域为
上的值域为 ,若存在,求出a的值;若不存在,请说明理由.
,若存在,求出a的值;若不存在,请说明理由.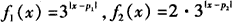 (x∈R,p1,p2为常数),函数f(x)定义为:对每个给定的实数x,
(x∈R,p1,p2为常数),函数f(x)定义为:对每个给定的实数x,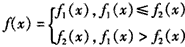 。
。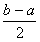 (闭区间[m,n]的长度定义为n-m)。
(闭区间[m,n]的长度定义为n-m)。