题目内容
已知函数![]() 在
在![]() 上为增函数,且
上为增函数,且![]() ,
,![]() 为常数,
为常数,![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 在
在![]()
![]() 上为单调函数,求
上为单调函数,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若在
,若在![]() 上至少存在一个
上至少存在一个![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
解:(1)由题意:![]() 在
在![]() 上恒成立,即
上恒成立,即![]()
![]() 在
在![]() 上恒成立,
上恒成立,
只需sin![]() …………
…………![]() (4分)
(4分)
(2) 由(1),得f(x)-g(x)=mx-![]() ,
,![]() ,由于f(x)-g(x)在其定义域内为单调函数,则
,由于f(x)-g(x)在其定义域内为单调函数,则![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,故
上恒成立,故![]() ,综上,m的取值范围是
,综上,m的取值范围是![]() …………(9分)
…………(9分)
(3)构造函数F(x)=f(x)-g(x)-h(x),![]() ,
,
当![]() 由
由![]() 得,
得,![]() ,所以在
,所以在![]() 上不存在一个
上不存在一个![]() ,使得
,使得![]() ; …………(12分)
; …………(12分)
当m>0时,![]() ,因为
,因为![]() ,所以
,所以![]() 在
在![]() 上恒成立,故F(x)在
上恒成立,故F(x)在![]() 上单调递增,
上单调递增,![]() ,故m的取值范围是
,故m的取值范围是![]() …………(15分)
…………(15分)
另法:(3)![]() 令
令![]()
![]()
![]()

练习册系列答案
相关题目
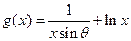 在
在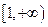 上为增函数,其中
上为增函数,其中 ,
,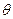 的取值集合;
的取值集合;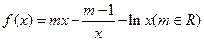 ,若
,若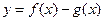 在
在 在
在 上为增函数,则实数a的取值范围为___________;
上为增函数,则实数a的取值范围为___________; 在
在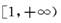 上为增函数,且
上为增函数,且
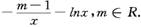
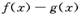 在[1,+
在[1,+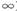 )上为单调函数,求m的取值范围;
)上为单调函数,求m的取值范围;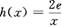 ,若在[1,e]上至少存在一个x0,使得
,若在[1,e]上至少存在一个x0,使得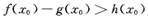 成立,求m的取值范围.
成立,求m的取值范围. 在
在 上为增函数,且
上为增函数,且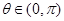 ,
,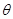 为常数,
为常数, .
.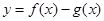 在
在 ,若在
,若在 上至少存在一个
上至少存在一个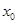 ,使得
,使得 成立,求的m取值范围.
成立,求的m取值范围. 在
在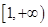 上为增函数,且
上为增函数,且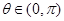 ,
,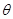 为常数,
为常数,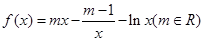 .
. 在
在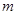 的取值范围;
的取值范围;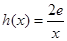 ,若在
,若在 上至少存在一个
上至少存在一个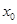 ,使得
,使得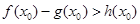 成立,求
成立,求