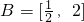题目内容
设函数y=log2(mx2-2x+2)定义域为A,集合B=[
,2]
(1)A=R,求m的取值范围,
(2)A∩B≠∅,求m的取值范围
(3)log2(mx2-2x+2)>2在B上恒成立,求m的取值范围.
| 1 |
| 2 |
(1)A=R,求m的取值范围,
(2)A∩B≠∅,求m的取值范围
(3)log2(mx2-2x+2)>2在B上恒成立,求m的取值范围.
(1)∵函数y=log2(mx2-2x+2)定义域为R
∴mx2-2x+2>0在R上恒成立
当m=0时,x<1,不在R上恒成立,故舍去
当m≠0时
解得m>
∴A=R,求m的取值范围(
,+∞)
(2)∵A∩B≠∅,
∴mx2-2x+2>0在集合B=[
,2]上有解
∴-
<
-
在集合B=[
,2]上有解
∴-
<(
-
)max=2
即m>-4
(3)∵log2(mx2-2x+2)>2在B上恒成立
∴mx2-2x-2>0在集合B=[
,2]上恒成立
∴
>
+
在集合B=[
,2]上恒成立
即
>(
+
)max=6
∴m>12
∴mx2-2x+2>0在R上恒成立
当m=0时,x<1,不在R上恒成立,故舍去
当m≠0时
|
| 1 |
| 2 |
∴A=R,求m的取值范围(
| 1 |
| 2 |
(2)∵A∩B≠∅,
∴mx2-2x+2>0在集合B=[
| 1 |
| 2 |
∴-
| m |
| 2 |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| 2 |
∴-
| m |
| 2 |
| 1 |
| x2 |
| 1 |
| x |
即m>-4
(3)∵log2(mx2-2x+2)>2在B上恒成立
∴mx2-2x-2>0在集合B=[
| 1 |
| 2 |
∴
| m |
| 2 |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| 2 |
即
| m |
| 2 |
| 1 |
| x2 |
| 1 |
| x |
∴m>12

练习册系列答案
相关题目