题目内容
已知函数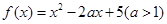 .
.
(1)若函数 的定义域和值域均为
的定义域和值域均为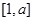 ,求实数
,求实数 的值;
的值;
(2)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的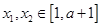 ,总有
,总有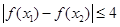 ,求实数
,求实数 的取值范围;
的取值范围;
(1)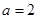 ;(2)
;(2)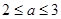 .
.
解析试题分析:(1)确定函数的对称轴,从而可得函数的单调性,利用 的定义域和值域均是
的定义域和值域均是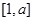 ,建立方程,即可求实数
,建立方程,即可求实数 的值;(2)由函数的单调性得出
的值;(2)由函数的单调性得出 在
在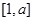 单调递减,在
单调递减,在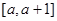 单调递增,从而求出
单调递增,从而求出 在
在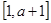 上的最大值和最小值的极差,使
上的最大值和最小值的极差,使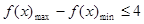 ,进而求出实数
,进而求出实数 的取值范围.
的取值范围.
试题解析:(1)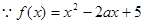 在
在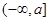 上的减函数,
上的减函数,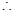
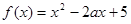 在
在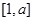 上单调递减
上单调递减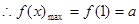 且
且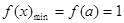
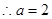 4分
4分
(2)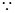
 在区间
在区间 上是减函数,
上是减函数,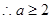 6分
6分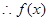 在
在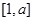 上单调递减,在
上单调递减,在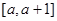 上单调递增
上单调递增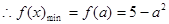 ,
,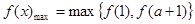
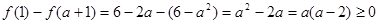
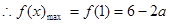 8分
8分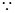 对任意的
对任意的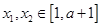 ,总有
,总有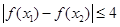
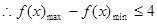 , 10分
, 10分
即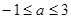 又
又 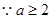 ,
,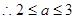 12分
12分
考点:二次函数的最值问题,考查函数的单调性.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
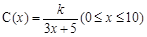 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
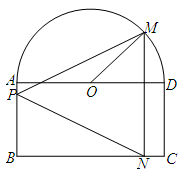
为隔热层建造费用与20年的能源消耗费用之和.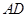 为半圆的直径,
为半圆的直径,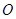 为半圆的圆心,
为半圆的圆心, ,
,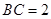 ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形 ,其底边
,其底边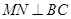 .
.
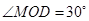 ,求三角形铁皮
,求三角形铁皮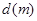 与车速
与车速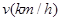 和车长
和车长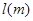 的关系满足:
的关系满足: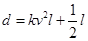 (
( 为正的常数),假定车身长为
为正的常数),假定车身长为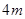 ,当车速为
,当车速为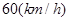 时,车距为2.66个车身长.
时,车距为2.66个车身长.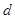 关于车速
关于车速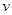 的函数关系式;
的函数关系式; (单位:千克)与销售价格
(单位:千克)与销售价格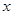 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式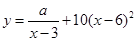 ,其中
,其中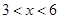 ,
, 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.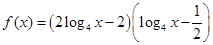 。
。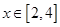 时,求该函数的值域;
时,求该函数的值域; 对于
对于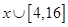 恒成立,求
恒成立,求 有取值范围。
有取值范围。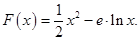
 的最小值;
的最小值;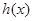 和
和 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数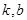 ,使得不等式
,使得不等式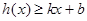 和
和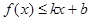 都成立,则称直线
都成立,则称直线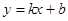 是函数
是函数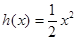 ,
,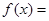
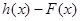 ,试问函数
,试问函数 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.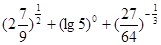 ;(2)解方程:log3(6x-9)=3.
;(2)解方程:log3(6x-9)=3.