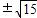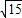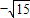Question

设z=log₂（m²-3m-3）+i log₂（m-3） （m∈R），若z对应点在直线x-2y+1=0上，则m的值是

 

．

Answer 1

分析：复数z对应的点在直线x-2y+1=0上，就是点的坐标适合方程，解方程求出满足定义域的解即可．

解答：解：设z=log₂（m²-3m-3）+ilog₂（m-3）（m∈R），若z对应点在直线x-2y+1=0上，
则log₂（m²-3m-3）-2log₂（m-3）+1=0
故2（m²-3m-3）=（m-3）²
∴m=

15

或m=-

15

（不适合）．
故答案为：

15

点评：本题考查复数的基本概念，对数的运算性质，是基础题．