题目内容
已知数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() (1)求数列
(1)求数列![]() 的通项公式;(2)设数列
的通项公式;(2)设数列![]() 满足:
满足:![]() ,且
,且![]() ,求证:
,求证:![]() ;(3)求证:
;(3)求证:![]() 。
。
(Ⅰ) ![]() (Ⅱ) 见解析 (Ⅲ)见解析
(Ⅱ) 见解析 (Ⅲ)见解析
解析:
:(1)当![]() 时,
时,![]() ,
,
![]() ,可得:
,可得:![]() ,
,
![]() .
.![]()
![]()
可得,![]() ……………………….4分
……………………….4分
(2)![]() 当
当![]() 时,
时,![]() ,不等式成立.
,不等式成立.
![]() 假设当
假设当![]() 时,不等式成立,即
时,不等式成立,即![]() 那么,当
那么,当![]() 时,
时,
![]()
所以当![]() 时,不等式也成立。
时,不等式也成立。
根据(![]() ),(
),(![]() )可知,当
)可知,当![]() 时,
时,![]() …………………9分
…………………9分
(3)设![]()
![]() 在
在![]() 上单调递减,
上单调递减,![]()
∵当![]() 时,
时,![]()
![]() ,
,
![]()
![]()
![]() ………………………14分
………………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 求使不等式
求使不等式 的前n项和为
的前n项和为 ,
, 且满足
且满足 +n (n>1且n∈
+n (n>1且n∈ )
) ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值  的前n项和为
的前n项和为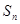 ,且
,且 ,
, ,并猜想
,并猜想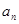 的表达式。
的表达式。