题目内容
已知 ,
, ,
, .
.
(1)当 时,试比较
时,试比较 与
与 的大小关系;
的大小关系;
(2)猜想 与
与 的大小关系,并给出证明.
的大小关系,并给出证明.
(1)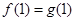 ,
, ,
,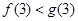 ;(2)猜想:对一切
;(2)猜想:对一切 ,
,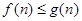 ,证明详见解析.
,证明详见解析.
解析试题分析:(1)由 的公式分别计算出
的公式分别计算出 时的
时的 及
及 的值,进而可得比较它们的大小关系;(2)用数学归纳法证明,由(1)可知,
的值,进而可得比较它们的大小关系;(2)用数学归纳法证明,由(1)可知,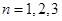 时,不等式显然成立,接着假设
时,不等式显然成立,接着假设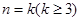 时不等式成立,进而只须证明
时不等式成立,进而只须证明 时不等式也成立即可,在证明
时不等式也成立即可,在证明 时,又只须将
时,又只须将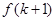 变形为
变形为 ,之后只须用比较法比较判断
,之后只须用比较法比较判断 与
与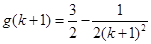 大小,即可证明本题.
大小,即可证明本题.
(1) 当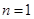 时,
时,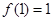 ,
,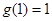 ,所以
,所以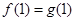 1分
1分
当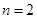 时,
时,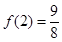 ,
,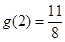 ,所以
,所以 2分
2分
当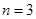 时,
时,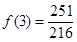 ,
,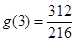 ,所以
,所以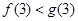 4分
4分
(2) 由(1),猜想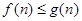 ,下面用数学归纳法给出证明 6分
,下面用数学归纳法给出证明 6分
①当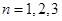 时,不等式显然成立 7分
时,不等式显然成立 7分
②假设当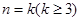 时不等式成立,即
时不等式成立,即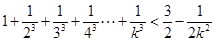 9分
9分
那么,当 时,
时,  11分
11分
因为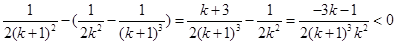 14分
14分
所以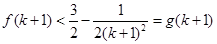 15分
15分
由①、②可知,对一切 ,都有
,都有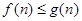 成立 16分.
成立 16分.
考点:数学归纳法.

练习册系列答案
相关题目
 的前
的前 项和为
项和为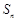 ,且满足
,且满足
 .
. ,
, ,
, ,
, 的值并写出其通项公式;
的值并写出其通项公式; 是一个自然数,
是一个自然数, 是
是 :
: 是自然数,
是自然数, (
( ,
, ).
). ,
, ;
; ,求证:
,求证: ;
; ,使得
,使得 .
. 中,已知
中,已知 ,
, ,
, (
( ,
, ).
). ,
,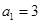 时,分别求
时,分别求 的值,判断
的值,判断 是否为定值,并给出证明;
是否为定值,并给出证明; ,使得
,使得 为完全平方数.
为完全平方数. ,即当
,即当 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*). ;
; ;
; ;
; .
. ,且
,且 ,求证:
,求证:
 ,考查
,考查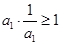 ;
; ;
; .
. 都成立的类似不等式,并用数学归纳法加以证明.
都成立的类似不等式,并用数学归纳法加以证明.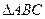 的三边长分别为
的三边长分别为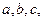 内切圆半径为
内切圆半径为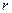 ,则三角形面积为
,则三角形面积为 ”,拓展到空间,类比上述结论,“若四面体
”,拓展到空间,类比上述结论,“若四面体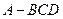 的四个面的面积分别为
的四个面的面积分别为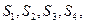 内切球的半径为
内切球的半径为