题目内容
已知函数f（x）=x|1-x|（x∈R），则不等式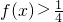
的解集为
- A.
- B.
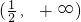
- C.
- D.
D
分析：可通过对x分x≥1与x＜1分类讨论，去掉绝对值符号，再解不等式即可．
解答：∵f（x）=x|1-x|=
，
∴当x＜1时，f（x）＞
?x-x2＞?（2x-1）2＜0，
∴x∈∅；
当x≥1时，f（x）＞?x2-x＞?（2x-1）2＞2，
∴x≥
或x＜
（舍去）．
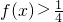∴则不等式的解集为[，+∞）．
故选D．
点评：本题考查绝对值不等式的解法，过对x分x≥1与x＜1分类讨论，去掉绝对值符号是关键，属于中档题．
分析：可通过对x分x≥1与x＜1分类讨论，去掉绝对值符号，再解不等式即可．
解答：∵f（x）=x|1-x|=
，∴当x＜1时，f（x）＞
?x-x2＞?（2x-1）2＜0，∴x∈∅；
当x≥1时，f（x）＞
?x2-x＞?（2x-1）2＞2，∴x≥
或x＜（舍去）．∴则不等式
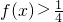的解集为[，+∞）．故选D．
点评：本题考查绝对值不等式的解法，过对x分x≥1与x＜1分类讨论，去掉绝对值符号是关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|