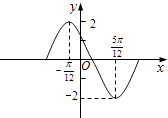题目内容
【题目】已知椭圆
上一点
与椭圆右焦点的连线垂直于x轴，直线l：y＝kx＋m与椭圆C相交于A，B两点(均不在坐标轴上)．
(1)求椭圆C的标准方程；
(2)设O为坐标原点，若△AOB的面积为
，试判断直线OA与OB的斜率之积是否为定值？若是请求出，若不是请说明理由．
【答案】（1）
；（2）定值
【解析】
(1)根据条件，代入已知点，和a,b,c的关系式，解得参数值，进而得到椭圆方程；（2）联立直线和椭圆方程得到二次方程，由三角形的面积得到4k2＋3－2m2＝0，kOA·kOB=
，根据韦达定理得到结果即可.
(1)由题意知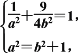
解得
∴椭圆C的标准方程为
＋
＝1．
(2)设点A(x1，y1)，B(x2，y2)，
由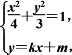
得(4k2＋3)x2＋8kmx＋4m2－12＝0，
由Δ＝(8km)2－16(4k2＋3)(m2－3)＞0，得m2＜4k2＋3．
∵x1＋x2＝
，x1x2＝
，
∴S△OAB＝
|m||x1－x2|＝|m|·
＝
，
化简得4k2＋3－2m2＝0，满足Δ＞0，从而有4k2－m2＝m2－3(*)，
∴kOA·kOB＝
＝
＝
＝
，由(*)式，得
＝1，
∴kOA·kOB＝－
，即直线OA与OB的斜率之积为定值－．
练习册系列答案
阅读快车系列答案
相关题目
