题目内容
设函数f(x)=|x-a|+3x,其中a>0.(Ⅰ)当a=1时,求不等式的f(x)≥3x+2解集;
(Ⅱ)若不等式f(x)≤0的解集为{x|x≤-1},求a的值.
【答案】分析:(Ⅰ)当a=1时,f(x)≥3x+2可化为|x-1|≥2.直接求出不等式f(x)≥3x+2的解集即可.
(Ⅱ)由f(x)≤0得|x-a|+3x≤0分x≥a和x≤a推出等价不等式组,分别求解,然后求出a的值.
解答:解:(Ⅰ)当a=1时,f(x)≥3x+2可化为|x-1|≥2.
由此可得 x≥3或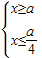 .
.
故不等式f(x)≥3x+2的解集为{x|x≥3或x≤-1}.
(Ⅱ) 由f(x)≤0得:|x-a|+3x≤0
此不等式化为不等式组: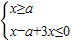 或
或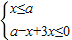 .
.
即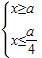 或
或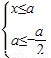
因为a>0,所以不等式组的解集为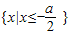 ,由题设可得
,由题设可得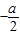 =-1,故a=2.
=-1,故a=2.
点评:本题是中档题,考查绝对值不等式的解法,注意分类讨论思想的应用,考查计算能力,常考题型.
(Ⅱ)由f(x)≤0得|x-a|+3x≤0分x≥a和x≤a推出等价不等式组,分别求解,然后求出a的值.
解答:解:(Ⅰ)当a=1时,f(x)≥3x+2可化为|x-1|≥2.
由此可得 x≥3或
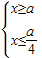 .
.故不等式f(x)≥3x+2的解集为{x|x≥3或x≤-1}.
(Ⅱ) 由f(x)≤0得:|x-a|+3x≤0
此不等式化为不等式组:
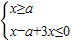 或
或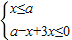 .
.即
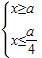 或
或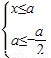
因为a>0,所以不等式组的解集为
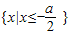 ,由题设可得
,由题设可得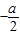 =-1,故a=2.
=-1,故a=2.点评:本题是中档题,考查绝对值不等式的解法,注意分类讨论思想的应用,考查计算能力,常考题型.

练习册系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|