题目内容
（本题满分14分）如图，已知在三棱柱ABC—A1B1C1中，AA1⊥面ABC，
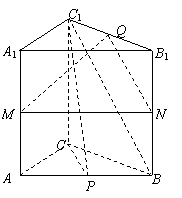AC=BC，M、N、P、Q分别是AA1、BB1、AB、B1C1的中点．
（1）求证：平面BPC1∥平面MNQ．
（2）求证：平面PCC1⊥平面MNQ；
解：（1）∵M、N 是AA1、BB1中点
∴MN∥PB
又因为MN
平面BPC1，PB
平面BPC1
所以MN∥平面BPC1 …………………………3分
同理可证：NQ∥BPC1 …………………………5分
又因为MN、NQ平面MNQ，MN∩NQ=N …………………………6分
所以平面BPC1∥平面MNQ …………………………7分
（2）∵AA1⊥面ABC，AA1∥C C1
∴C C1⊥面ABC
又∵AB面ABC
∴C C1⊥AB …………………………9分
∵AC=BC， P分别是AB1的中点．
∴PC⊥AB …………………………10分
又因为C C1、PC平面PCC1，C C1∩PC=C
所以AB⊥平面PCC1 …………………………11分
又∵AB∥MN
∴MN⊥平面PCC1 …………………………13分
又因为MN平面MNQ
所以平面PCC1⊥平面MNQ …………………………14分
，E是棱CC1上动点，F是AB中点，
；
、
的边长都是1，平面
平面
在
上移动，点
在
上移动，若
（
）
的长；
为何值时，
与面
所成锐二面角余弦值的大小.
，又E、F分别是C1A和C1B的中点。
（1）求证：EF//平面ABC；
平面C1CBB1；