题目内容
如图，在矩形ABCD中，BD为对角线，AE⊥BD，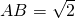
，AD=1，则BE=
- A.1
- B.
- C.
- D.
B
分析：矩形各内角为直角，在直角△ABD中，已知AB、AD，根据勾股定理即可求BD的值，根据直角三角形的射影定理，即可求解BE．
解答：矩形各内角为直角，∴△ABD为直角三角形
在直角△ABD中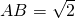，，AD=1，
则BD=
=
，
再由射影定理，得AB2=BE×BD
∴
故选B．
点评：本题考查了勾股定理在直角三角形中的运用，考查了直角三角形的射影定理，本题中根据勾股定理求BD的值是解题的关键．
分析：矩形各内角为直角，在直角△ABD中，已知AB、AD，根据勾股定理即可求BD的值，根据直角三角形的射影定理，即可求解BE．
解答：矩形各内角为直角，∴△ABD为直角三角形
在直角△ABD中，
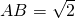，AD=1，则BD=
=，再由射影定理，得AB2=BE×BD
∴
故选B．
点评：本题考查了勾股定理在直角三角形中的运用，考查了直角三角形的射影定理，本题中根据勾股定理求BD的值是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在矩形ABCD中，AB=2BC，P，Q分别为线段AB，CD的中点，EP⊥平面ABCD．
如图，在矩形ABCD中，已知AB=2AD=4，E为AB的中点，现将△AED沿DE折起，使点A到点P处，满足PB=PC，设M、H分别为PC、DE的中点．
如图，在矩形ABCD中，AB=3
如图，在矩形ABCD中，已知AB=3，AD=1，E、F分别是AB的两个三等分点，AC，DF相交于点G，建立适当的平面直角坐标系：
如图，在矩形ABCD中，AB=