题目内容
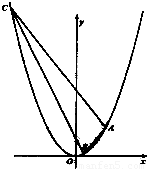
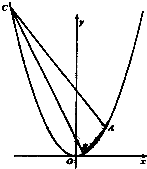 已知点A(m,4)(m>0)在抛物线x2=4y上,过点A作倾斜角互补的两条直线l1和l2,且l1,l2与抛物线另一个交点分别为B、C.
已知点A(m,4)(m>0)在抛物线x2=4y上,过点A作倾斜角互补的两条直线l1和l2,且l1,l2与抛物线另一个交点分别为B、C.(I)求证:直线BC的斜率为定值;
(II)若抛物线上存在两点关于直线BC对称,求|BC|的取值范围.
分析:(I)根据点A(m,4)(m>0)在抛物线x2=4y上,确定A的坐标,设B(x1,y1),C(x2,y2),利用kAB+kAC=0,kBC=
,即可得解;
(II)设直线BC的方程为y=-2x+b,P(x3,y3),Q(x4,y4)关于直线BC对称,确定PQ中点M的坐标,利用M在抛物线内部,确定b的范围,进一步计算|BC|,即可得到结论.
| x1+x2 |
| 4 |
(II)设直线BC的方程为y=-2x+b,P(x3,y3),Q(x4,y4)关于直线BC对称,确定PQ中点M的坐标,利用M在抛物线内部,确定b的范围,进一步计算|BC|,即可得到结论.
解答:(I)证明:∵点A(m,4)(m>0)在抛物线x2=4y上,∴m=4
设B(x1,y1),C(x2,y2),则kAB+kAC=
+
=0
∴x1+x2=-8
∴kBC=
=-2
∴直线BC的斜率为定值-2;
(II)解:设直线BC的方程为y=-2x+b,P(x3,y3),Q(x4,y4)关于直线BC对称,
设PQ中点M(x0,y0),则kPQ=
=
=
,
∴x0=1,故M(1,-2+b)
∵M在抛物线内部,
∴-2+b>
,解得b>
y=-2x+b代入抛物线可得x2+8x-4b=0,
∴x3+x4=-8,x3x4=-4b
∴|BC|=
|x3-x4|=
×
>10
∴|BC|的取值范围为(10
,+∞).
设B(x1,y1),C(x2,y2),则kAB+kAC=
| x1+4 |
| 4 |
| x2+4 |
| 4 |
∴x1+x2=-8
∴kBC=
| x1+x2 |
| 4 |
∴直线BC的斜率为定值-2;
(II)解:设直线BC的方程为y=-2x+b,P(x3,y3),Q(x4,y4)关于直线BC对称,
设PQ中点M(x0,y0),则kPQ=
| x3+x4 |
| 4 |
| x0 |
| 2 |
| 1 |
| 2 |
∴x0=1,故M(1,-2+b)
∵M在抛物线内部,
∴-2+b>
| 1 |
| 4 |
| 9 |
| 4 |
y=-2x+b代入抛物线可得x2+8x-4b=0,
∴x3+x4=-8,x3x4=-4b
∴|BC|=
| 1+4 |
| 5 |
| 64+16b |
| 5 |
∴|BC|的取值范围为(10
| 5 |
点评:本题考查直线的斜率,考查点关于直线的对称性,解题的关键是正确求斜率,利用弦长公式计算弦长,属于中档题.

练习册系列答案
相关题目
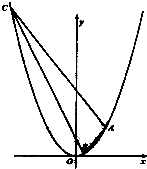 已知点A(m,4)(m>0)在抛物线x2=4y上,过点A作倾斜角互补的两条直线l1和l2,且l1,l2与抛物线另一个交点分别为B、C.
已知点A(m,4)(m>0)在抛物线x2=4y上,过点A作倾斜角互补的两条直线l1和l2,且l1,l2与抛物线另一个交点分别为B、C.