题目内容
在平面直角坐标系中,已知点P(1,-1),过点P作抛物线T:y=x2的切线,其切点分别为M(x1,y1)、N(x2,y2)(其中x1<x2).(Ⅰ)求x1与x2的值;
(Ⅱ)若以点P为圆心的圆E与直线MN相切,求圆E的面积;
(Ⅲ)过原点O(0,0)作圆E的两条互相垂直的弦AC,BD,求四边形ABCD面积的最大值.
【答案】分析:(Ⅰ)由y=x2先求出y′=2x.再由直线PM与曲线T相切,且过点P(1,-1),得到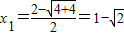 ,或
,或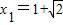 .同理可得
.同理可得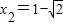 ,或
,或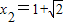 ,然后由x1<x2知
,然后由x1<x2知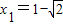 ,
,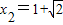 .
.
(Ⅱ)由题意知,x1+x2=2,x1•x2=-1,则直线MN的方程为:2x-y+1=0.再由点P到直线MN的距离即为圆E的半径,可求出圆E的面积.
(Ⅲ)四边形ABCD的面积为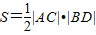 ,设圆心E到直线AC的距离为d1,垂足为E1,圆心E到直线BD的距离为d2,垂足为E2;
,设圆心E到直线AC的距离为d1,垂足为E1,圆心E到直线BD的距离为d2,垂足为E2;
由此可求出四边形ABCD面积的最大值.
解答:解:(Ⅰ)由y=x2可得,y′=2x.(1分)
∵直线PM与曲线T相切,且过点P(1,-1),
∴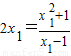 ,即x12-2x1-1=0,
,即x12-2x1-1=0,
∴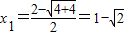 ,或
,或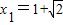 ,(3分)
,(3分)
同理可得: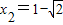 ,或
,或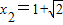 (4分)
(4分)
∵x1<x2,∴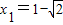 ,
,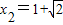 .(5分)
.(5分)
(Ⅱ)由(Ⅰ)知,x1+x2=2,x1•x2=-1,
则直线MN的斜率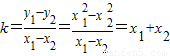 ,--(6分)
,--(6分)
∴直线M的方程为:y-y1=(x1+x2)(x-x1),又y1=x12,
∴y-x12=(x1+x2)x-x12-x1x2,即2x-y+1=0.(7分)
∵点P到直线MN的距离即为圆E的半径,即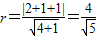 ,(8分)
,(8分)
故圆E的面积为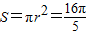 .(9分)
.(9分)
(Ⅲ)四边形ABCD的面积为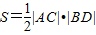
不妨设圆心E到直线AC的距离为d1,垂足为E1;
圆心E到直线BD的距离为d2,垂足为E2;
则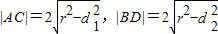 ,(10分)
,(10分)
由于四边形EE1OE2为矩形.且d12+d22=|OE|2=(1-0)2+(-1-0)2=2(11分)
所以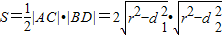
由基本不等式2ab≤a2+b2可得
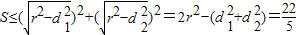 ,
,
当且仅当d1=d2时等号成立.(14分)
注:(Ⅲ)解法较多,阅卷时可酌情给分.
点评:本题考查直线和圆锥轼线的位置关系,解题时要认真审题,仔细解答.
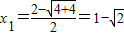 ,或
,或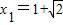 .同理可得
.同理可得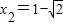 ,或
,或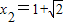 ,然后由x1<x2知
,然后由x1<x2知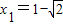 ,
,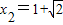 .
.(Ⅱ)由题意知,x1+x2=2,x1•x2=-1,则直线MN的方程为:2x-y+1=0.再由点P到直线MN的距离即为圆E的半径,可求出圆E的面积.
(Ⅲ)四边形ABCD的面积为
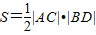 ,设圆心E到直线AC的距离为d1,垂足为E1,圆心E到直线BD的距离为d2,垂足为E2;
,设圆心E到直线AC的距离为d1,垂足为E1,圆心E到直线BD的距离为d2,垂足为E2;由此可求出四边形ABCD面积的最大值.
解答:解:(Ⅰ)由y=x2可得,y′=2x.(1分)
∵直线PM与曲线T相切,且过点P(1,-1),
∴
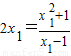 ,即x12-2x1-1=0,
,即x12-2x1-1=0,∴
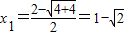 ,或
,或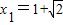 ,(3分)
,(3分)同理可得:
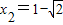 ,或
,或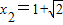 (4分)
(4分)∵x1<x2,∴
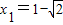 ,
,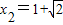 .(5分)
.(5分)(Ⅱ)由(Ⅰ)知,x1+x2=2,x1•x2=-1,
则直线MN的斜率
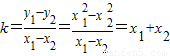 ,--(6分)
,--(6分)∴直线M的方程为:y-y1=(x1+x2)(x-x1),又y1=x12,
∴y-x12=(x1+x2)x-x12-x1x2,即2x-y+1=0.(7分)
∵点P到直线MN的距离即为圆E的半径,即
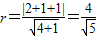 ,(8分)
,(8分)故圆E的面积为
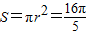 .(9分)
.(9分)(Ⅲ)四边形ABCD的面积为
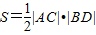
不妨设圆心E到直线AC的距离为d1,垂足为E1;
圆心E到直线BD的距离为d2,垂足为E2;
则
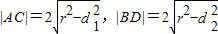 ,(10分)
,(10分)由于四边形EE1OE2为矩形.且d12+d22=|OE|2=(1-0)2+(-1-0)2=2(11分)
所以
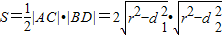
由基本不等式2ab≤a2+b2可得
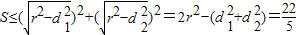 ,
,当且仅当d1=d2时等号成立.(14分)
注:(Ⅲ)解法较多,阅卷时可酌情给分.
点评:本题考查直线和圆锥轼线的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
相关题目