题目内容
2.将函数y=f(x)的图象先向左平移$\frac{π}{4}$个单位,然后向上平移1个单位,得到函数y=2cos2x的图象,则f(x-$\frac{7π}{2}$)是( )| A. | -sin2x | B. | -2cosx | C. | 2sinx | D. | 2cosx |
分析 由函数图象平移结合倍角公式可得f(x+$\frac{π}{4}$)=cos2x,利用换元法求出f(x),则f(x-$\frac{7π}{2}$)可求.
解答 解:由题意可得,f(x+$\frac{π}{4}$)+1=2cos2x,
∴f(x+$\frac{π}{4}$)=2cos2x-1=cos2x,
令x+$\frac{π}{4}$=t,则x=t-$\frac{π}{4}$,
∴f(t)=cos(2t-$\frac{π}{2}$)=sin2t,即f(x)=sin2x,
∴f(x-$\frac{7π}{2}$)=sin(2x-7π)=-sin2x.
故选:A.
点评 本题考查y=Asin(ωx+φ)型函数的图象变换,训练了函数解析式的求法,是基础题.

练习册系列答案
相关题目
10.平面内,点P在以O为顶点的直角内部,A,B分别为两直角边上两点,已知$|{\overrightarrow{OP}}|=2$,$\overrightarrow{OP}•\overrightarrow{OA}=2$,$\overrightarrow{OP}•\overrightarrow{OB}=1$,则当|AB|最小时,sin∠AOP=( )
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
7.已知函数f(x)=x2-x+2,则${∫}_{0}^{1}$f(x)dx=( )
| A. | $\frac{13}{6}$ | B. | $\frac{11}{6}$ | C. | 2 | D. | 3 |
14.已知函数f(x)=sin(ωx+φ)(ω>0),若f(x)的图象向左平移$\frac{π}{3}$个单位所得的图象与f(x)的图象右平移$\frac{π}{6}$个单位所得的图象重合,则ω的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
| A. | y=x3 | B. | $y=|{log_2^{\;}x}|$ | C. | y=2|x| | D. | y=-x2+1 |
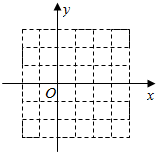 设实数x,y满足$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-4≥0\\ 2y-3≤0\end{array}\right.$(注:图中的正方形网格的边长为1个单位长度).
设实数x,y满足$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-4≥0\\ 2y-3≤0\end{array}\right.$(注:图中的正方形网格的边长为1个单位长度).