题目内容
14.已知函数f(x)=sin(ωx+φ)(ω>0),若f(x)的图象向左平移$\frac{π}{3}$个单位所得的图象与f(x)的图象右平移$\frac{π}{6}$个单位所得的图象重合,则ω的最小值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由题意将f(x)的图象向左平移$\frac{π}{3}$个单位所得的图象与f(x)的图象右平移$\frac{π}{6}$个单位所得的图象重合,说明两个函数相位差是2π的整数倍,求出ω的值即可.
解答 解:∵将函数f(x)=sin(ωx+φ)的图象向左平移$\frac{π}{3}$个单位,所得的图象解析式为:y=sin(ωx+$\frac{π}{3}$ω+φ),
将函数f(x)的图象右平移$\frac{π}{6}$个单位所得的图象解析式为:y=y=sin(ωx-$\frac{π}{6}$ω+φ),
若所得图象重合,
∴$\frac{π}{3}$ω+$\frac{π}{6}$ω=2kπ,k∈Z,解得ω=4k,k∈Z,
∵ω>0,可解得ω的最小值为4.
故选:C.
点评 本题考查三角函数的周期、图象变换等基础知识,相位差是函数周期的整数倍,是本题解题关键.

练习册系列答案
相关题目
2.将函数y=f(x)的图象先向左平移$\frac{π}{4}$个单位,然后向上平移1个单位,得到函数y=2cos2x的图象,则f(x-$\frac{7π}{2}$)是( )
| A. | -sin2x | B. | -2cosx | C. | 2sinx | D. | 2cosx |
4.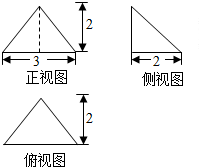 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )
 若某多面体的三视图如图所示,则此多面体的表面积是( )
若某多面体的三视图如图所示,则此多面体的表面积是( )| A. | 6 | B. | 18 | C. | 8+3$\sqrt{2}$ | D. | 3+4$\sqrt{13}$ |
 若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.
若执行如图伪代码时没有执行y←x2+1,则输入的x的取值范围是x>2.5.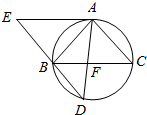 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$.